Identité Remarquable Trigonométrique

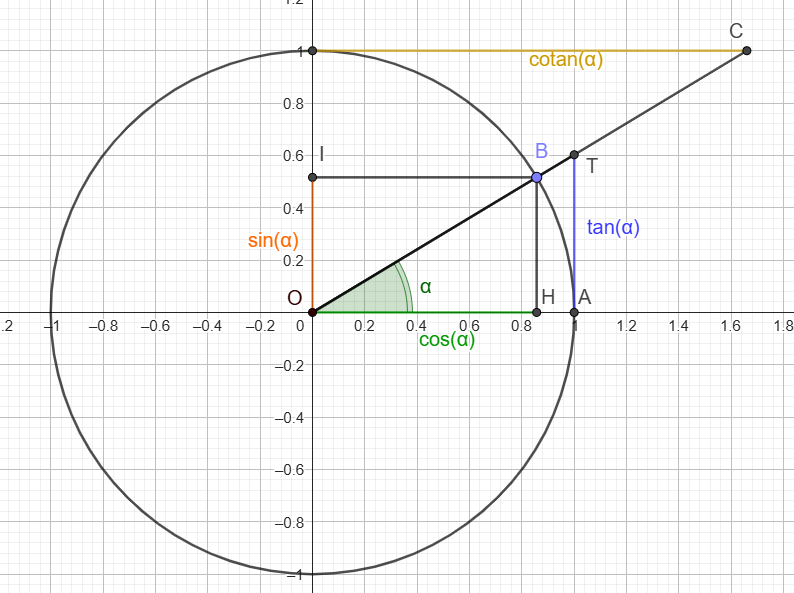
Appliquons le Théorème de Pythagore dans le triangle (OHB). Alors:

• \(OB² = OH² + HB² = OH² + OI² = cos²\alpha + sin²\alpha\) 
• \(OB²=1\) car dans le cercle Unité, le rayon r =1.

Et pour finir:

\[\boxed{ \begin{align*} cos²\alpha + sin²\alpha = 1 \end{align*}}\]

Connaissances:

• identité remarquable: \(\begin{align*} cos²\alpha+sin²\alpha=1 \end{align*}\)
• Définition: \(\begin{align*} tan\alpha=\frac{sin\alpha}{cos\alpha} \end{align*}\)
• Définition: \(\begin{align*} sec\alpha=\frac{1}{cos\alpha} \end{align*}\)

En divisant l'identité remarquable par \(cos²\alpha\) des 2 côtés:

\(\begin{align*}1+\frac{sin²\alpha}{cos²\alpha}=\frac{1}{cos²\alpha} \Leftrightarrow 1+tan²\alpha=\frac{1}{cos²\alpha}=sec²\alpha \end{align*}\)

\[\boxed{1+tan²\alpha=\frac{1}{cos²\alpha}}\]

Connaissances:

• identité remarquable: \(cos²\alpha+sin²\alpha=1\)
• Définition: \(\begin{align*} cotan\alpha=\frac{cos\alpha}{sin\alpha}= \frac{1}{tan\alpha} \end{align*}\)
• Définition: \(\begin{align*} csc\alpha=\frac{1}{sin\alpha} \end{align*}\)

En divisant l'identité remarquable par \(sin²\alpha\) des 2 côtés:

\(\begin{align*}\frac{cos²\alpha}{sin²\alpha}+1=\frac{1}{sin²\alpha} \Leftrightarrow 1+cotan²\alpha=\frac{1}{sin²\alpha}=csc²\alpha \end{align*}\)

\[\boxed{1+cotan²\alpha=\frac{1}{sin²\alpha}}\]