Partie A :

\[\forall n \in \mathbb N, I_n = \int_0^{\pi/2} cos^nt.dt\]

1. Etudier la monotonie de la suite \((I_n)_{(n \in \mathbb N)}\)
2. Calculs
   1. Calculer \(I_0\)
   2. Calculer \(I_1\)
3. Démontrer à l'aide d'une IPP que \(\forall n \in \mathbb N\), \((n+2)I_{n+2}= (n+1)I_n\)
4. En déduire que \(\forall n \in \mathbb N, (n+1)I_{n+1}I_n = \pi/2 \)
5. Démontrer en utilisant les questions 1 et 3 que \(\lim\limits_{n \mapsto + \infty}\frac{I_{n-1}}{I_n}=1\)
6. Démonstrations
   1. Démontrer que si \(n \to + \infty\) alors \(I_n\) à pour  équivalent    \( \sqrt{\frac{\pi}{2n}}\)
   2. En déduire que la suite \(I_n\) converge et préciser sa limite
7. Démontrer que \(\begin{align*}\forall n \in \mathbb N, I_{2n} = \prod_{k=0}^{n-1}\frac{2k+1}{2k+2} \times \frac{\pi}{2} = \frac{(2n)!}{[2^n.n!]²}\frac{\pi}{2} \end{align*}\)
8. Déduire des questions 6 et 7 que \(\forall n \in \mathbb N, \lim\limits_{n \to + \infty}\frac{1 \times 3 \dots \times (2n+1)}{2 \times 4\times \dots \times 2n}\frac{1}{\sqrt n}=\frac{2}{\sqrt\pi}\)

Partie B:

Pour la suite, on pose:\[\forall n \in \mathbb N,  \forall x \in ]-\pi/2;\pi/2[, F_n(x)=\int_0^xtan^nt.dt\]

1. Calculer \(F_1(x)\) et \(F_2(x)\) \(\forall x \in ]-\pi/2;\pi/2[\)
2. Soient \(n \in \mathbb N,\) et \(x \in ]-\pi/2;\pi/2[\), démontrer que \(F_{n+2}(x)+F_n(x)=\frac{tan^{n+1}x}{n+1}\)
3. En déduire la valeur de \(F_4(x), \forall x \in ]-\pi/2;\pi/2[\)
4. On pose: \(\forall n \in \mathbb N, J_n=\int_0^{\pi/4}tan^nt.dt = F_n(\pi/4)\)
   Etudier la monotonie de \((J_n)_{n \in \mathbb N}\). \(J_n\) est elle convergente?
5. Soit \(a \in ]0;\pi/4[\), montrer que\((\frac{\pi}{4}-a) tan^na \leq J_n \leq a.tan^na+(\frac{\pi}{4}-a)\)
6. On note \(\forall n \in \mathbb N , U_n=\frac{(-1)^n}{2n+1}\) et \(.(S_n)_{n \in \mathbb N}\) la suite des sommes partielles de \(U_n\)
   1. En utilisant la question 10, montrer que , \(\forall n \in \mathbb N, S_n = \sum_{k=0}^n(-1)^k(J_{2k}+ J_{2k+2})\)
   2. En déduire que \(\forall n \in \mathbb N, S_n= \pi/4+(-1)^nJ_{2n+2}\)
   3. La série \(\sum U_n\) est elle convergente? Si oui quelle est sa somme?

\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(cost)^n dt\end{align*}\)

• La fonction \(x \mapsto cos(x)\) est de classe \(C^1\) sur l'intervalle \([0;\pi/2]\)
  • Elle est continue , et dérivable sur cet intervalle
  • Sa dérivée est continue donc primitivable
• \(\forall n \space \in \mathbb N\), La fonction \(x \mapsto (cos(x)^n\) est aussi de classe \(C^1\) sur l'intervalle \([0;\pi/2]\)

• \(\begin{align*}\forall n \in \mathbb N \end{align*}\),  \(\begin{align*} I_n=\int_0^{\pi/2}(cost)^n dt \end{align*}\) existe

 Sur \([0; \pi/2]\), la fonction \( t \mapsto cos(t)\) est:

• continue, donc \(t \mapsto cos^nt\) est continue, donc intégrable
• \(>0\) et n 'est pas identiquement nulle, donc \(t \mapsto \int cos^nt.dt\) est \(> 0\)
• et:
  \(\begin{align*} & 0 \leq cos(t)  \leq 1 \\
  \Rightarrow  &0 \leq cos^{n+1}t  \leq cos^nt  \\
  \Rightarrow &0 < \int_0^{\pi/2}cos^{n+1}t.dt  \leq \int_0^{\pi/2}cos^nt.dt \\
  \Rightarrow &0 < I_{n+1}  \leq I_n
  \end{align*}\)

La suite \((I_n)_{(n \in \mathbb N)}\) est décroissante et \(I_n >0\)

\(\begin{align*}I_0 & = \int_0^{\pi/2}cos^nt.dt 
 = \int_0^{\pi/2}cos^0t.dt \\
& = \int_0^{\pi/2}1 \times dt 
 = \big[t \big]_0^{\pi/2} 
 = \pi/2
\end{align*}\)

\[ \boxed{I_0 = \pi/2}\]

\(\begin{align*}I_1 & = \int_0^{\pi/2}cos^nt.dt = \int_0^{\pi/2}cos^1t.dt \\
& = \int_0^{\pi/2}cost.dt = \big[sint \big]_0^{\pi/2}  = 1-0=1
\end{align*}\)

\[ \boxed{I_1 = 1}\]

\(\forall n \in \mathbb N\),

\(\begin{align*}I_{n+2} & = \int_0^{\pi/2}cos^{n+2}t.dt \\
& = \int_0^{\pi/2}\big[ cost \times cos^{n+1}t\big].dt \\
& \begin{cases} u' =cost \\ v= cos^{n+1}t \end{cases} \Rightarrow
\begin{cases} u =sint \\ v'=(n+1)(cost^nt)(-sint) \end{cases} \\
I_{n+2} & = \underbrace{\big[sint \times cos^{n+1}t\big]_0^{\pi/2}}_{=0} -  \int_0^{\pi/2}\big[sint \times (n+1) \times  cos^{n}t \times (-sint)\big].dt \\
& = (n+1)\int_0^{\pi/2} sin²t  \times  cos^{n}t.dt \\
& = (n+1)\int_0^{\pi/2} (1-cos²t)  \times  cos^{n}t.dt \\
& = (n+1)\int_0^{\pi/2} cos^{n}t.dt- (n+1)\int_0^{\pi/2}cos²t  \times  cos^{n}t.dt \\
& = (n+1)\int_0^{\pi/2} cos^{n}t.dt- (n+1)\int_0^{\pi/2} cos^{n+2}t.dt \\
& = (n+1)I_n - (n+1)I_{n+2} \\
\Rightarrow & I_{n+2}+ (n+1)I_{n+2} = (n+1)I_n \\
\Rightarrow & (n+2)I_{n+2}=(n+1)I_n
\end{align*}\)

\[\boxed{\forall n \in \mathbb N, (n+2)I_{n+2}= (n+1)I_n}\]

Soit \(U_n\) telle que \( \forall n \in \mathbb N, U_n= (n+1)I_{n+1}I_n\)

\(\begin{align*} U_{n+1} & = (n+2)I_{n+2}I_{n+1} \\
& = (\cancel{n+2}) ( \frac{n+1}{\cancel{n+2}}I_n)I_{n+1} \\
& = (n+1)I_{n+1}I_n = U_n \end{align*}\)

\(\begin{align*}\forall n \in \mathbb N, U_{n+1}= U_n  \end{align*}\) donc la suite \(U_n\) est constante et :
\(U_0 = (0+1)I_1I_0=1 \times 1 \times \pi/2 = \pi/2 \)

\[\boxed{\forall n \in \mathbb N, (n+1)I_{n+1}I_n = \pi/2} \]

• question 1 : \(\forall n \in \mathbb N, I_n\) est décroissante et \(I_n>0\), donc \(I_n \neq 0\). On peut alors diviser par \(I_n\).
  \(\Rightarrow I_{n-2} \leq I_{n-1} \leq I_{n}\)
  \(\Rightarrow \frac{I_{n-2}}{I_{n}} \leq \frac{I_{n-1}}{I_{n}} \leq \frac{I_{n}}{I_{n}}\)
  \(\Rightarrow \frac{I_{n-2}}{I_{n}} \leq \frac{I_{n-1}}{I_{n}} \leq 1\)
• question 3 : \(\forall n \in \mathbb N, (n+2)I_{n+2}= (n+1)I_n\)
  \(\Rightarrow(n)I_{n}= (n-1)I_{n-2}\)
  \(\Rightarrow  \frac{I_{n-2}}{I_{n}}=\frac{n}{(n-1)} \)

On en déduit que \(\frac{n}{(n-1)} \leq \frac{I_{n-1}}{I_{n}} \leq 1\)

Or \(\lim\limits_{n \to + \infty}\frac{n}{n-1}=1\) et par le Théorème des gendarmes, on obtient:

\[\boxed {\lim\limits_{n \mapsto + \infty}\frac{I_{n-1}}{I_n}=1}\]

• question 4: \(\forall n \in \mathbb N, (n+1)I_{n+1}I_n = \pi/2 \)
  • \(n+1 \space\space\widetilde{+\infty}\space\space n\)
• question 3: \(I_n>0\)
• question 5:  \(\lim\limits_{n \to + \infty}\frac{I_{n-1}}{I_n}=1\)
  • donc \(I_{n+1} \space\space\widetilde{+\infty}\space\space I_n \)

Il vient alors :

\(\begin{align*} & (n+1) I_nI_{n+1} = \pi/2 \\
\Rightarrow & n(I_n)² \space\space\widetilde{+\infty}\space\space \pi/2  
\Rightarrow (I_n)² \space\space\widetilde{+\infty}\space\space \pi/2n \\
 \Rightarrow & \lvert I_n \rvert \space\space\widetilde{+\infty}\space\space \sqrt{\pi/2n}  
\Rightarrow  I_n \space\space\widetilde{+\infty}\space\space \sqrt{\pi/2n} \end{align*}\)

\[\boxed{I_n \space\space\widetilde{+\infty}\space\space {+ \infty} \sqrt{\frac{\pi}{2n}} }\]

• question 1 : \(I_n\) est décroissante et \(I_n>0\)
• question 6a: \(I_n \space\space\widetilde{+\infty}\space\space\sqrt{\frac{\pi}{2n}}\)

La suite \(I_n\) est décroissante et \(I_n>0\), et d'après le Théorème des suites monotones bornées:  \(I_n\) converge.

Comme \(I_n \space\space\widetilde{+\infty}\space\space \sqrt{\frac{\pi}{2n}}\)

\(\lim\limits_{n \to + \infty}I_n=\lim\limits_{n \to + \infty}\sqrt{\frac{\pi}{2n}}=0\)

\[ \boxed{I_n\text{ converge et }\lim\limits_{n \to + \infty}I_n=0}\]

• question 3 : \(\forall n \in \mathbb N, (n+2)I_{n+2}= (n+1)I_n \Rightarrow I_{n+2}=\frac{n+1}{n+2}I_n\)

\(\begin{align*} \Leftrightarrow I_{nombre} & =\frac{nombre-1}{nombre} \times I_{nombre-2} \\
\Leftrightarrow I_{2n} & =\frac{2n-1}{2n}I_{2n-2} \text{ avec }n \neq 0 \\
& =\frac{2n-1}{2n} \times\frac{2n-3}{2n-2} I_{2n-4} \\
& =\frac{2n-1}{2n} \times\frac{2n-3}{2n-2}\times\frac{2n-5}{2n-4} I_{2n-6} \\
& =\frac{2n-1}{2n} \times\frac{2n-3}{2n-2}\times \dots \frac{1}{2} I_{0} \\
& = \frac{impairs}{pairs}I_0 \\
&=\frac{\prod_{k=0}^{n-1}2k+1}{\prod_{k=0}^{n-1}2k+2} \times I_0 \\
I_{2n} & =\prod_{k=0}^{n-1} \frac{2k+1}{2k+2}\times \frac{\pi}{2} \\
&\text{En multipliant numérateur et dénominateur par les nombres paires : } \\
& = \frac{(2n)(2n-1)(2n-3)(2n-4)\dots (3)(2)(1)}{\big[ \underbrace { (2n)(2n--2)(2n-4)\dots (4)(2)}_{\text{n fois le facteur }2}\big]^2}I_0 \\
& = \frac{(2n)!}{\big[ 2^n \times (n(n-1)(n-2) \dots (2)(1)\big]^2} I_0\\
& = \frac{(2n)!}{\big[ 2^n \times n!\big]^2} \frac{\pi}{2}\\ \\ \\
\text{Avec }n=0: \\
I_0 & = \int_0^{\pi/2} cos^0t.dt = \pi/2 \\
I_0 & = \frac{(2 \times 0)!}{\big[2^0 \times 0!\big]^2} \times \pi/2 \\
& = \frac{0!}{[1 \times 1]^2}\times \pi/2 = \pi/2
\end{align*}\)

\[ \boxed{\begin{align*} \forall n \in \mathbb N, I_{2n}  =\prod_{k=0}^{n-1} \frac{2k+1}{2k+2}\times \frac{\pi}{2} = \frac{(2n)!}{\big[ 2^n \times n!\big]^2} \frac{\pi}{2}  \end{align*}}\]

• question 6 : \(I_n\text{ converge et }\lim\limits_{n \to + \infty}I_n=0\) et \(I_n \space\space\widetilde{+\infty}\space\space \sqrt{\frac{\pi}{2n}}\)
• question 7 : \(I_{2n}  =\prod_{k=0}^{n-1} \frac{2k+1}{2k+2}\times \frac{\pi}{2}\)

\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} F_n(x)=\int_0^{x}tan^nt dt\end{align*}\)

• La fonction \(x \mapsto tan(x)\) est de classe \(C^1\) sur l'intervalle \(]-\pi/2;\pi/2[\)
  • Elle est continue , et dérivable sur cet intervalle
  • Sa dérivée est continue donc primitivable
• \(\forall n \space \in \mathbb N\), La fonction \(x \mapsto tan^n(x)\) est aussi de classe \(C^1\) sur l'intervalle \(]-\pi/2;\pi/2[\)

• \(\begin{align*}\forall n \in \mathbb N \end{align*}\),  \(\begin{align*} F_n(x)=\int_0^{x}tan^nt .dt \end{align*}\) existe

\(\forall x \in ]-\pi/2;\pi/2[\), la fonction \(x \mapsto tan(x)\) est continue. Il en est de même pour la fonction \(x \mapsto tan^nx, \forall n \in \mathbb N\). En conséquence, \(\int_0^xtan^nt.dt\) existe.

\[\boxed{\forall x \in ]-\pi/2;\pi/2[ \text{ et } \forall n \in \mathbb N, F_n(x) \text{  existe.} }\]

\(\begin{align*}F_1(x) & =\int_0^xtan(t).dt \\
& = \int_0^x \frac{sint}{cost}.dt 
= \big[ -ln \lvert cos t \rvert\big]_0^x \\
& = -ln \lvert cos x \rvert  \text{ et }cos(x) > 0\text{ sur } ]-\pi/2;\pi/2[ \\
 & = -ln( cos x)  \end{align*}\)

\[\boxed {\forall x \in ]-\pi/2;\pi/2[, F_1(x)=-ln(cos(x)) } \]

\(\begin{align*}F_2(x) & =\int_0^xtan^2t.dt 
 = \int_0^x \frac{sin²t}{cos²t}.dt \\
& = \int_0^x \frac{1-cos²t}{cos²t}.dt 
= \int_0^x (\frac{1}{cos²t}-1).dt \\
& = \int_0^x \frac{1}{cos²t}dt - \int_0^x1 \times dt \\
& = \big[ tan(t)\big]_0^x - \big[x \big]_0^x 
= tan(x) -x
 \end{align*}\)

\[\boxed {\forall x \in ]-\pi/2;\pi/2[, F_2(x)= tan(x) -x }\]

\(\forall n \in \mathbb{N^*}\)

\( \begin{align*} F_{n+2}(x)+F_n(x) & = \int_0^xtan^{n+2}t.dt+\int_0^xtan^nt.dt \\
& = \int_0^x(tan^{n+2}t+tan^nt)dt \\
& = \int_0^xtan^nt(tan^2t+1)dt \\
& = \int_0^{tanx} u^n \times u'.du \\
& = \bigg[\frac{u^{n+1}}{n+1} \bigg]_0^{tanx} 
= \frac{tan^{n+1}x}{n+1} \\ \\
\end{align*}\)

Pour \(n=0\) 

\(\begin{align*} F_2(x)+ F_0(x) & =\frac{tan^{0+1}x}{0+1}= tanx\end{align*}\)

\(\begin{align*} F_2(x)+ F_0(x) & = \overbrace{tanx-x}^{F_2(x)} + \overbrace{ \int_0^xtan^0tdt}^{F_0(x)} \\  
& = tanx-x + \int_0^x1\times dt \\
& = tanx-x + \big[x\big]_0^x \\
& = tanx-x + x = tanx \end{align*}\)

On en conclue que :

\[\boxed {\forall n \in \mathbb N, \text{ et }\forall x \in ]-\pi/2;\pi/2[, F_{n+2}(x)+F_n(x) = \frac{tan^{n+1}x}{n+1} }\]

\(\forall n \in \mathbb N, \text{ et } \forall x \in ]-\pi/2;\pi/2[, \)

\(\begin{align*}& && F_{n+2}(x)+F_n(x) && = \frac{tan^{n+1}x}{n+1} \\
& \Rightarrow && F_4(x)+F_2(x) && = \frac{tan^{3}x}{3} \\
& \Rightarrow && F_4(x) && = \frac{tan^{3}x}{3} - F_2(x)\\
& && && = \frac{tan^{3}x}{3}-[tan(x) -x] \\
& &&  &&= \frac{tan^{3}x}{3}-tan(x) +x
\end{align*}\)

\[\boxed { \forall x \in ]-\pi/2;\pi/2[, F_4(x)=\frac{tan^{3}x}{3}-tan(x) +x }\]

Pour  \(x \in [0;\pi/4]\) on a \(\forall n \in \mathbb N\):

 \(\begin{align*} 0 & \leq tan x \leq 1 \\
0 & \leq tan^nx \leq 1\\
\Rightarrow 0 & \leq tan^{n+1}x \leq tan^nx\end{align*}\)

Par positivité de l'intégrale, il vient \(J_{n+1} <J_{n}\)
Donc \(J_n\) est décroissante et \(J_n \gt 0\)

• Théorème des suites monotones bornée: \(\Rightarrow J_n\) converge 

\[\boxed{\begin{align*} \begin{cases} J_n \searrow \\ J_n \geq0 \end{cases}
\Rightarrow J_n \text{ converge.}
\end{align*}}\]

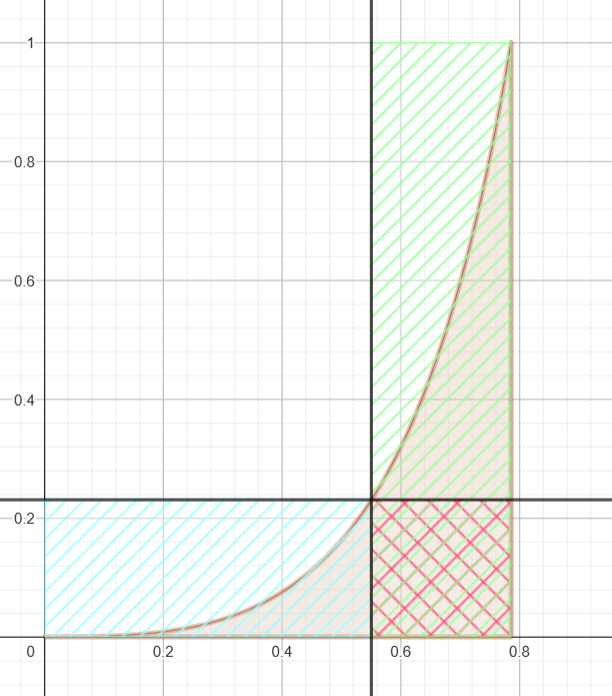
Le sujet nous intime fortement de couper notre intégrale en 2 parties grace à la relation de Chasles. Il vient alors:

\( \begin{align*}\int_0^{a} tan^nt.dt+ \int_a^{\pi/4} tan^nt.dt = J_n =  \int_0^{a} tan^nt.dt +\int_a^{\pi/4} tan^nt.dt
\end{align*}\)

Plusieurs remarques: \( \forall n \in \mathbb N\) 

• sur \(a \in ]0;\pi/4[\) on a :
  
  • \(tan^n a \nearrow\)
  • \(0 < tan a <1 \Rightarrow 0 < tan^n a < 1 \)

\( \begin{align*} \overbrace{\int_0^{a} tan^nt.dt}^{>0}+ \int_a^{\pi/4} tan^nt.dt = &  J_n =  \underbrace{\overbrace{\int_0^{a} tan^nt.dt}^{\leq (a-0)tan^na}}_{\text{carré bleu}} +\underbrace{\overbrace{\int_a^{\pi/4} tan^nt.dt}^{(\pi/4-a)tan^n1}}_{\text{carré vert}} \\
\underbrace{ \overbrace{\int_a^{\pi/4} tan^nt.dt}^{(\pi/4-a)tan^na}}_{\text{carré rouge}} \leq & J_n \leq  a tan^n a +(\pi/4-a) \\
(\pi/4-a)tan^na \leq & J_n \leq  a tan^n a +(\pi/4-a) \\
\end{align*}\)

Il vient :

\[ \boxed { \begin{align*}\forall a \in ]0;\pi/4[, (\pi/4-a)tan^na \leq & J_n \leq  a tan^n a +(\pi/4-a) \end{align*}}\] 

\(J_n\) prendra sa valeur si \( a \to \pi/4\)  sans atteindre \(\pi/4\), et alors, 
\(\begin{align*} \begin{cases}tan a <1 \Rightarrow \lim\limits_{n \to \infty} tan^na = 0 \\ \lim\limits_{a \to pi/4}\pi/4-a=0 \end{cases}  \end{align*}\)

Il résulte que :\(\lim (\pi/4-a)tan^na \leq \lim J_n \leq \lim a tan^n a +(\pi/4-a)\) avec 

\(\begin{align*} \begin{cases}\lim (\pi/4-a)tan^na=0 \\
\lim a tan^n a +(\pi/4-a)=0
\end{cases}  \end{align*}\)

Et par le Théorème des gendarmes :

\[\boxed{\lim (J_n)_{n \in \mathbb N}=0}\]

Rappels:

• \(\begin{align*} \forall n \in \mathbb N,  \forall x \in ]-\pi/2;\pi/2[, F_n(x)=\int_0^xtan^nt.dt \end{align*}\)
• \(\begin{align*}\forall n \in \mathbb N, \text{ et }\forall x \in ]-\pi/2;\pi/2[, F_{n+2}(x)+F_n(x) = \frac{tan^{n+1}x}{n+1} \end{align*}\) 
• \(\begin{align*} \forall n \in \mathbb N, J_n=\int_0^{\pi/4}tan^nt.dt = F_n(\pi/4) \end{align*}\)

En conséquence: \(\begin{align*} \forall n \in \mathbb N, J_{2k+2}+ J_{2k}=\frac{tan^{2k+1}\pi/4}{2k+1} = \frac{1}{2k+1}  \end{align*}\)

Et \(\begin{align*} \forall n \in \mathbb N , U_n=\frac{(-1)^n}{2n+1} = (-1)^n(J_{2k+2}+ J_{2k}) \end{align*}\)

On en conclue que \(\begin{align*} S_n = \sum_{k=0}^n U_n = \sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k})\end{align*}\)

\[ \boxed{\forall n \in \mathbb N, S_n =\sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k})}\]

\( \begin{align*}\forall n \in \mathbb N, S_n =\sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k}) \end{align*}\)

\(\begin{align*} & n = 0 && (-1)^0 (J_2+J_0) && = && \cancel{+J_2} &&+ J_0 \\
& n = 1 && (-1)^1 (J_4+J_2) && = && \cancel{-J_4}  &&\cancel{-J_2} \\
& n = 2 && (-1)^2 (J_6+J_4) && = && \cancel{+J_6}  &&\cancel{+J_4} \\
& n = 3 && (-1)^3 (J_8+J_6) && = && \cancel{-J_8}  &&\cancel{-J_6} \\
& \vdots && \vdots && \vdots && \vdots && \vdots\\
& \vdots && \vdots && \vdots && \vdots && \vdots\\
& n = n && (-1)^n (J_{2n+2}+J_{2n}) && = && (-1)^nJ_{2n+2}  &&\cancel{(-1)^nJ_{2n}} \\ \\
& S_n && && = && (-1)^nJ_{2n+2} && +J_0 
\end{align*}\)

Avec:

\(\begin{align*} J_0 = \int_0^{\pi/4}tan^0t.dt = \pi/4\end{align*}\)

Et pour finir, on a:

\[ \boxed {\forall n \in \mathbb N, S_n= \pi/4+(-1)^nJ_{2n+2}}\]