Ces formules de l'angle moitié sont souvent trés utiles losqu'on calcule des intégrales comportant des fonctions trigonométriques. En effet , dans certains cas, on est amené à procéder au changement de variable:\(t=tan(\frac{x}{2})\) C 'est la raison pour laquelle iront jusqu'au calcul de \(dx\).
- Préliminaires
- sinx en fonction de t
- cosx en fonction de t
- tanx en fonction de t
- dx en fonction de t
- résumé
Préliminaires
|
Il est donc possible de dessiner un triangle rectangle tel que : \(tan\frac{x}{2}=t=\frac{t}{1}\) \(CAH-SOH-TOA \Rightarrow \begin{cases} \text{angle:}(x/2) \\ \text{côté opposé =}t \\ \text{côté adjascent =}1 \end{cases}\) Calcul de l'hypoténuse L : \(L²=1²+t² \Rightarrow L=\sqrt{1+t²}\) \(\Rightarrow \begin{cases} tan(\frac{x}{2}) = \frac{t}{1} \\ cos(\frac{x}{2}) = \frac{1}{\sqrt{1+t²}} \\ sin(\frac{x}{2}) = \frac{t}{\sqrt{1+t²}} \end{cases}\) |
sinx en fonction de t = tan(x/2)
|
Connaissance pour la démonstration:
\(\begin{align*} sinx & =sin(\frac{x}{2}+\frac{x}{2}) \\ |
cosx en fonction de t=tan(x/2)
|
Connaissance pour la démonstration:
\(\begin{align*}cosx & =cos(\frac{x}{2}+\frac{x}{2}) \\ |
tanx en fonction de t=tan(x/2)
|
Connaissance pour la démonstration:
\(\begin{align*} \\ \[\boxed{tanx=\frac{2t}{1-t²}} \] |
\(dx\) en fonction de t=tan(x/2)
|
\(t= tan(x/2) \Longrightarrow x=2.arctan(t)\) avec \(\big( arctan(t) \big )' = \frac{1}{1+t²} \Rightarrow dx=2.\frac{1}{1+t^2}.dt\) \[\Longrightarrow \boxed{ dx=\frac{2}{1+t²}.dt}\] |
résumé
| \[\boxed{\text{Si on pose } t= tan(x/2) \text{, alors: }\\ \begin{align*} sinx=\frac{2t}{1+t^2} && cosx=\frac{1-t^2}{1+t^2} && tanx = \frac{2t}{1-t^2} && dx=\frac{2}{1+t²}.dt \end{align*}}\] |

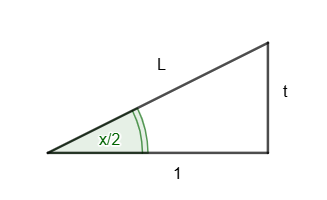 On pose \(t=tan\frac{x}{2}\)
On pose \(t=tan\frac{x}{2}\)