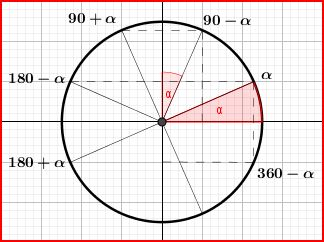
Dessinons maintenant le cercle unité avec plusieurs angles remarquables (\(\pi = 180°\)):
Ne pas hésiter à redessiner ce cercle trigonométrique, ou à se le remémorer, le visualiser, à chaque fois que vous en aurez besoin lors des exercices et devoirs.
|
\[-\alpha\] |
\[ cos(-\alpha)=cos(\alpha)\] paire |
\[sin (-\alpha)=-sin(\alpha) \] impaire |
|
|
\[\alpha + 2k\pi\] |
\[ cos(\alpha+ 2k\pi)=cos(\alpha)\] \(2\pi\) périodique |
\[sin (\alpha+ 2k\pi)=sin(\alpha) \] \(2\pi\) périodique |
|
| \[\pi-\alpha\] |
\[ cos(\pi-\alpha)=-cos(\alpha)\] |
\[sin (\pi-\alpha)=sin(\alpha)\] | |
| \[\pi+\alpha\] | \[ cos(\pi+\alpha)=-cos(\alpha)\] | \[sin (\pi+\alpha)=-sin(\alpha)\] | |
| \[\frac{\pi}{2}+\alpha\] | \[cos(\frac{\pi}{2}+\alpha)=-sin(\alpha)\] | \[sin(\frac{\pi}{2}+ \alpha)=cos(\alpha)\] | |
| \[\frac{\pi}{2}-\alpha\] | \[cos(\frac{\pi}{2}-\alpha)=sin(\alpha)\] | \[sin(\frac{\pi}{2} - \alpha)= cos(\alpha)\] |
Ces formules se retiennent facilement à condition de bien mémoriser la figure ci dessus avec les angles.
Elles ne seront alors pas reprises dans le précis de trigonométrie en fin de chapitre.