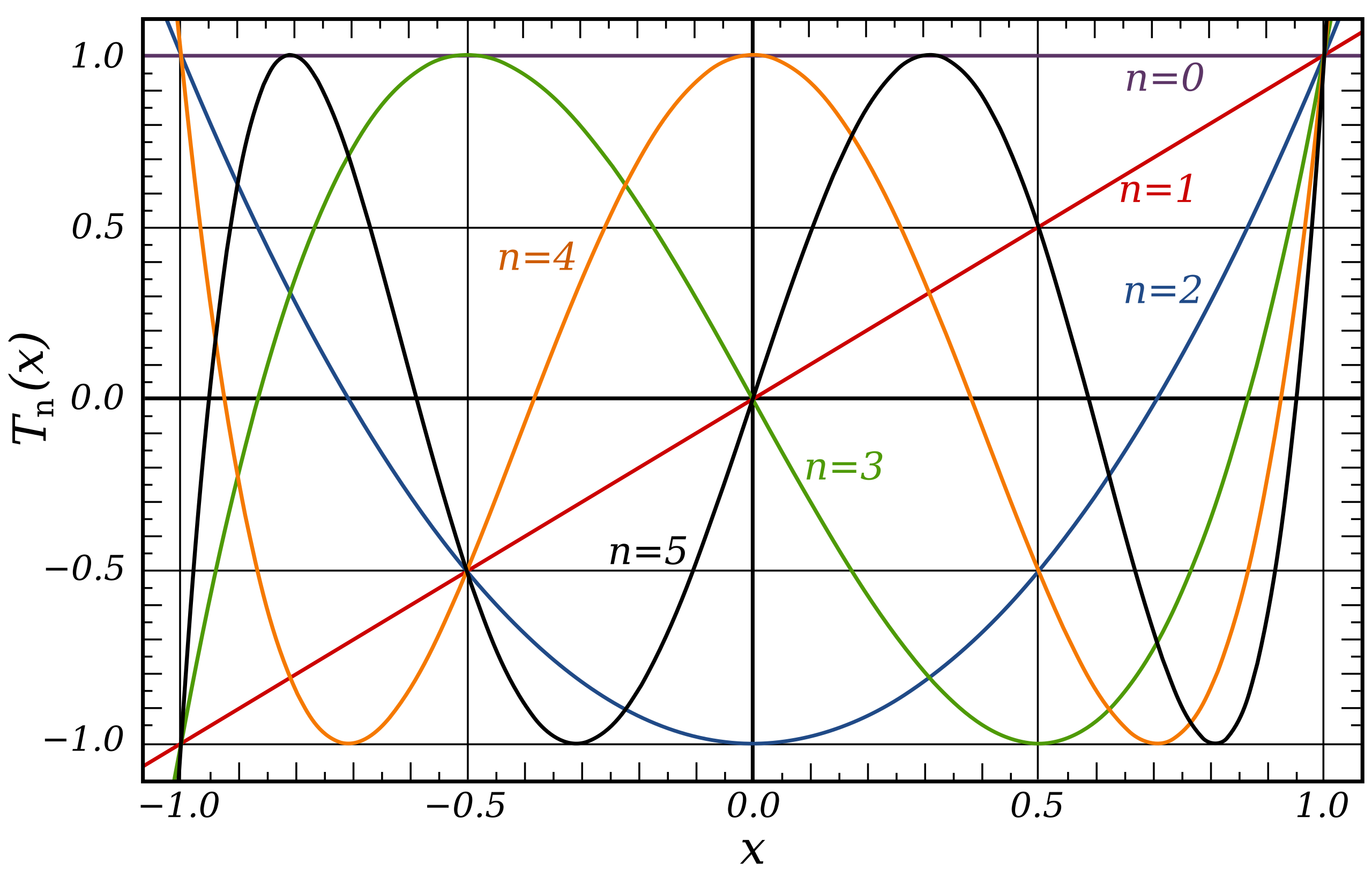
Sujet

Les polynômes de Tchebychev de première et de seconde espèce sont les polynômes $(T_n)_{n \in \mathbb N}$ et $ (U_n)_{n \in \mathbb N^*}$ définis par :
\[\boxed{ \cos(nt) = T_n(\cos t) \space \space \space\text{ et } \space \space \space \sin (nt) = \sin{t} .U_n(\cos t)}\]

Ils permettent de généraliser la linéarisation des formes $sin(nt)$ et $cos(nt)$.
Il peut être intéressant pour gagner en rapidité dans d 'autres exercices qui comporteraient ces formes trigonométriques de se rappeler des premiers polynômes, et de leurs différentes propriétés.

Donner les expression de $T_0$, $T_1$, $T_2$, $U_0$, $U_1$,$U_2$
Montrer que les $T_n$ et $U_n$ existent, sont uniques, et sont donnés par:
$\begin{align*} T_n(x) = \sum\limits_{k=0}^{\lfloor n/2 \rfloor} (-1)^k \binom{n}{2k} x^{n-2k}(1-x^2)^k \end{align*}$ et $\begin{align*} U_n(x) = \sum\limits_{k=0}^{\lfloor (n-1)/2 \rfloor} (-1)^k \binom{n}{2k+1} x^{n-2k-1}(1-x^2)^k \end{align*}$
Montrer que $\forall x \in [-1;1]$, $T_n(x) = cos(n.arccos(x))$ et $\forall x \in ]-1;1[$, $U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}}$
Montrer que $T'_n(x) = nU_n(x)$
Trouver une relation entre $T_{n+1}$, $T_{n}$, $T_{n-1}$
En déduire les degré et coefficient dominant de $T_n$. Puis confirmer les résultats a l'aide de la question 2
Montrer que $\forall n \in \mathbb N$, $T_n(x)$ a la même parité que $n$
Montrer que $\forall n \in \mathbb N$, $T_n(1)=1$ , $T'_n(1) = n^2$ , $T_n(0)=0$ si $n$ est impair, $T_n(0)=(-1)^{n/2}$ sinon
Montrer que pour $n \in \mathbb N^*$, $T_n$ possède $n$ racines simples $\begin{align*}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align*}$ et que $\begin{align*} \sum\limits_{k=0}^{n-1} x_k = 0 \end{align*}$
Trouver les EXTREMA de $T_n$
Montrer que $ \begin{align*} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align*}$
Montrer que $T_n$ est solution de l'équation différentielle: $(X^2-1)y" + Xy' - n^2y=0$
Soit $E$ le $\mathbb R$-espace vectoriel des fonctions continues de $[-1;1]$ dans $\mathbb R$. Justifier que l'application de $E^2 \to \mathbb R$ définie par $\langle f(t),g(t) \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt$ est un produit scalaire.
Pour tous $(m,n) \in \mathbb N^2$, calculer le produit scalaire $\langle T_n , T_m \rangle$. Que peut on dire de la famille $\big(T_n\big)_{n \in \mathbb N}$ ?
A partir du résultat de la question 4 et des autres résultats, déterminer les degré et coefficient dominant de $U_n$
Montrer que $\forall n \in \mathbb N, \exists t \in \mathbb R, \space cos t = \frac{sin[(n+1)t]}{sint}$
En déduire que $\big( U_n \big)_{n \in \mathbb N}$ suit aussi la relation de récurrence de la question 5, que $ \forall n \in \mathbb N, \space \space U_n$ est scindé simple sur $\mathbb R$, à racine dans $]-1;1[$, en précisant les racines

1 - Donner les expression de $T_0$, $T_1$, $T_2$, $T_3$, $U_1$,$U_2$, $U_3$

On utilise les formules de trigonométrie usuelles:
$\begin{align*} \begin{cases} cos^2t + sin^2t = 1 \\ cos(a+b) = cosa.cosb-sina.sinb \\ sin(a+b) = sina.cosb +cosa.sinb \\ sin(2a) = 2sina.cosa \end{cases} \end{align*}$

$T_n$ est définie pour $n \in \mathbb N$
$T_n(cost) = cos(nt)$

Calcul de $T_0$
$\begin{align*} T_0(cos t) & = cos(0 \times t) = 1 \\
& \Rightarrow \boxed { T_0(X) = 1 } \end{align*}$
Calcul de $T_1$
$\begin{align*} T_1(cos t) & = cos(1 \times t) = cost \\
& \Rightarrow \boxed{T_1(X) = X} \end{align*}$
Calcul de $T_2$
$\begin{align*} T_2(cos t) & = cos(2t) = cos(t+t) \\
& = cost \times cost - sint \times sint \\
& = cos^2t-sin^2t \\
& = cos^2t-(1-cos^2t) = 2cos^2t - 1 \\
&\Rightarrow \boxed{T_2(X) = 2X^2-1} \end{align*}$
Calcul de $T_3$
$\begin{align*} T_3(cos t ) & = cos(3t) = cos(2t+t) \\
& = cos(2t)cost -sin(2t)sint \\
& = T_2(cost) cost-2sint. cost. sint \\
& = (2cos^2t-1)cost- 2sin^2t.cost \\
& = 2cos^3t - cost -2(1-cos^2t)cost \\
& = 2cos^3t - cost+ 2cos^3t-2cost\\
& = 4cos^3t - 3cost \\
& \Rightarrow \boxed{T_3(X) = 4X^3-3X} \end{align*}$

$U_n$ est définie pour $n \in \mathbb N^*$
$sin(nt) = sint.U_n(cost)$

Calcul de $U_1$
$\begin{align*} sin(1t) & = sin(t) = sin(t) \times \underbrace{1} \\
& = sint \times \underbrace{U_1(cost)} \\
& \Rightarrow \boxed { U_1(X) = 1}\end{align*}$
Calcul de $U_2$
$\begin{align*} sin(2t) & = 2sin(t).(cost) \\
& = sint \times \underbrace{2cost} \\
& = sint \times \underbrace{U_2(cost)} \\
& \Rightarrow \boxed { U_2(X) = 2X}\end{align*}$
Calcul de $U_3$
$\begin{align*} sin(3t) & = sin(t+2t) \\
& = sint.cos(2t)-cost.sin(2t) \\
& = sin(t).T_2(cost) + cost.2sint.cost \\
& = sin(t).(2cos^2t-1) + 2sint.cos^2t \\
& = sint (2cos^2t-1+2cos^2t) \\
& = sint \times \underbrace{(4cos^2t-1)} \\
& = sint \times \underbrace{U_3(cost)} \\
& \Rightarrow \boxed { U_3(X) = 4X^2-1}\end{align*}$

2 - Montrer que les $T_n$ et $U_n$ existent, sont uniques, et sont donnés par:
$\begin{align} T_n(x) = \sum\limits_{k=0}^{\lfloor n/2 \rfloor} (-1)^k \binom{n}{2k} x^{n-2k}(1-x^2)^k \end{align}$ et $\begin{align} U_n(x) = \sum\limits_{k=0}^{\lfloor (n-1)/2 \rfloor} (-1)^k \binom{n}{2k+1} x^{n-2k-1}(1-x^2)^k \end{align}$

1 - Existence:

Pour montrer que $T_n$ et $ U_n$ existent, il suffit de les calculer.

Pour cela, nous utiliserons: $\begin{align*} \begin{cases} \text{La formule de Moivre: }(cosx + i.sinx)^n = cos(nx)+i.sin(nx) \\
\text{La formule d'Euler: }e^{ix} = cosx + i.sinx \\
\text{Le binôme de Newton: si(x,y) commutent, }(x+y)^n = \sum\limits_{k=0}^{n} \binom{n}{k}x^{k}y^{n-k} \end{cases} \end{align*}$

$\begin{align*} cos(nt)+i.sin(nt) & = e^{int}= {(e^{it})}^n = (cost + i.sint)^n \end{align*}$

$cost$ et $i.sint$ commutent, on peut appliquer la formule du binôme de Newton:

$\begin{align*} cos(nt)+i.sin(nt) & = (cost + i.sint)^n \\
& = \sum\limits_{p=0}^{n} \binom{n}{p}(cost)^{n-p}(i.sint)^{p} \\
& = \sum\limits_{p=0}^{n} \binom{n}{p}cos^{n-p}t.i^{p}.sin^{p}t \end{align*}$

L'expression ci-dessus contient une forme $i^p$ dont le résultat dépend de la parité de $p$. Il nous faut alors envisager 2 cas:

Si $p$ est pair : $p=2k$ et $i^p = i^{2k}={i^2}^k = (-1)^k$. Alors $cos(nt)+i.sin(nt)$ sera un réel.
Si $p$ est impair: $p=2k+1$ et $p=2k$ et $i^p = i^{2k+1}=i.{i^2}^k = (-1)^k.i$. Alors $cos(nt)+i.sin(nt)$ sera un imaginaire pur.

Cela nous amène à séparer cette somme en 2 sommes: une contenant les $p$ pairs et l'autre les $p$ impairs.

$\begin{align*} cos(nt)+i.sin(nt) & = \sum\limits_{p=0}^{n} \binom{n}{p}cos^{n-p}t.i^{p}.sin^{p}t \\
& = \underbrace{ \sum\limits_{0 \leq 2k \leq n} \binom{n}{2k}cos^{n-2k}t.i^{2k}.sin^{2k}t }_{p \text{ pairs}} + \underbrace{ \sum\limits_{0 \leq 2k+1 \leq n} \binom{n}{2k+1}cos^{n-(2k+1)}t.i^{2k+1}.sin^{2k+1} t}_{p \text{ impairs}} \\
& = \sum\limits_{0 \leq 2k \leq n} \binom{n}{2k}cos^{n-2k}t.(-1)^k.{(sin^{2}t)}^k + \sum\limits_{0 \leq 2k+1 \leq n} \binom{n}{2k+1}cos^{n-(2k+1)}t.\underbrace{i}.(-1)^k.\underbrace{sint} .{(sin^{2}t)}^k \\
& = \sum\limits_{0 \leq 2k \leq n} \binom{n}{2k} (-1)^k cos^{n-2k}t.{(1-cos^{2}t)}^k + i.sint \sum\limits_{0 \leq 2k+1 \leq n} \binom{n}{2k+1} (-1)^k cos^{n-2k-1}t.{(1-cos^{2}t)}^k \end{align*}$

Quand $p$ est pair ($p=2k$):
- La première valeur de $k$ est $0$ (donc $p=0$)
- si $n$ est pair (par exemple $22$), alors la dernière valeur de $k$ est $n/2$ (donc $11$) et $p = 2 \times 11=22)$
- si $n$ est impair (par exemple $23$), alors la dernière valeur de $k$ est $\lfloor n/2 \rfloor$ (donc $\lfloor 23/2 \rfloor = 11$) et $p = 2\times 11 + 1 = 23$
Quand $p$ est impair ($p=2k+1$):
- La première valeur de $k$ est $0$ (donc $p=1$)
- si$n$ est impair (par exemple $23$), alors la dernière valeur de $k$ est $(n-1)/2$ (donc $11$) et $p = 2\times 11 + 1 = 23$
- si $n$ est pair (par exemple $22$), alors la dernière valeur de $k$ est $\lfloor (n-1)/2 \rfloor$ (donc $\lfloor (22-1)/2 \rfloor = 10$) et $p = 2 \times 10=21)$

$\begin{align*} cos(nt)+i.sin(nt) & = \sum\limits_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} (-1)^k cos^{n-2k}t.{(1-cos^{2}t)}^k + i.sint \sum\limits_{k=0}^{\lfloor (n-1)2/ \rfloor} \binom{n}{2k+1} (-1)^k cos^{n-2k-1}t.{(1-cos^{2}t)}^k \end{align*}$

Et si $x = cost$, alors $\forall t \in \mathbb R,$ on a: $x \in [-1;1]$

$\begin{align*} cos(nt)+i.sin(nt) & = \sum\limits_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} (-1)^k x^{n-2k}.{(1-x^{2})}^k + i.sint \sum\limits_{k=0}{\lfloor (n-1)2/ \rfloor} \binom{n}{2k+1} (-1)^kx^{n-2k-1}.{(1-x^{2}t)}^k \\
& = T_n(cost) + i.sint.U_n(cost) \end{align*}$

$T_n$ et $U_n$ existent
\[ T_n(x) = \sum\limits_{k=0}^{ \lfloor n/2 \rfloor} {(-1)}^{k} \binom{n}{2k}x^{n-2k} \space {(1-x^2)}^k\]	\[U_n(X) = \sum\limits_{k=0}^{ \lfloor (n-1)/2 \rfloor} {(-1)}^{k} \binom{n}{2k+1}x^{n-2k-1} \space (1-x^2)^{k}\]

2 - Unicité

Supposons qu'il existe 1 autre polynômes $Q_n$ tel que $Q_n(x)$ soit égal à $cos(nt)$, alors:
$\begin{align*}\forall t \in \mathbb R, \space \space & T_n(cost) = Q_n (cost) \\
\Leftrightarrow & T_n(cost)- Q_n (cost) = 0 \\
\Leftrightarrow & (T_n- Q_n)(cost) = 0, \space \forall t \in \mathbb R \end{align*}$

Soit alors $x \in [-1;1]$, $\exists! \space t \in [0;\pi]$ tel que $x = cos (t)$ et en conséquence
$\begin{align*} (T_n- Q_n)(x) = 0 \space \space \forall x \in [-1;1]\end{align*}$

Il existe alors une infinité de racines de $(T_n- Q_n)$ sur $[-1;1]$ , et dans ce cas $(T_n- Q_n)$ est le polynôme identiquement nul.
Si $(T_n- Q_n)$ est le polynôme identiquement nul, alors:
$\begin{align*} (T_n- Q_n)(x) = 0 \space \space \forall x \in \mathbb R \\ \end{align*}$
et alors $\forall x \in \mathbb R, \space \space T_n = Q_n $ et $T_n$ est unique.

La démonstration est exactement la même pour $U_n$

3 - Conclusion :

$T_n$ et $U_n$ existent et sont uniques
\[ T_n(x) = \sum\limits_{k=0}^{ \lfloor n/2 \rfloor} {(-1)}^{k} \binom{n}{2k}x^{n-2k} \space {(1-x^2)}^k\]	\[U_n(X) = \sum\limits_{k=0}^{ \lfloor (n-1)/2 \rfloor} {(-1)}^{k} \binom{n}{2k+1}x^{n-2k-1} \space (1-x^2)^{k}\]

3 - Montrer que $\forall x \in [-1;1]$, $T_n(x) = cos(n.arccos(x))$ et $\forall x \in ]-1;1[$, $U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}}$

On sait $ \begin{align*} \begin{cases} \cos(nt) = T_n(\cos t) \\ \sin (nt) = \sin{t} .U_n(\cos t) \end{cases} \end{align*}$

Soit: $ \begin{align*} \begin{cases}x \in [-1;1] \\
t= arccos(x) \Rightarrow x=cost \text{ avec } \boxed{t \in [0;\pi]} \end{cases} \end{align*} $.
Alors:
$T_n(x) = T_n(cost) = cos(nt) = cos(n.arcos(x))$

De même, soit: $\begin{align*} \begin{cases} x \in ]-1;1[ \\
t= arccos(x) \Rightarrow x=cost \text{ avec } \boxed{t \in ]0;\pi[} \\ \text{Donc }sint \neq 0 \Rightarrow \text{ possibilité de diviser par }sint \\
sint \gt 0 \Rightarrow \text{ possibilité de mettre sous la racine } \end{cases} \end{align*}$.
Alors:
$\begin{align*}sin(nt) & = sint.U_n(cost) \\ \Rightarrow U_n(cost) & = U_n(x) = \frac{sin(nt)}{sint} = \frac{sin(n.arccos(x))}{\sqrt{sin^2t}} \\
& = \frac{sin(n.arcos(x))}{\sqrt{1-cos^2t}} = \frac{sin(n.(arcos(x))}{\sqrt{1-x^2}} \end{align*}$

\[\begin{align*} \forall x \in [-1;1] , \space \space T_n(x) = cos(n.arccos(x)) \end{align*}\]

\[\begin{align*} \forall x \in ]-1;1[ , \space \space U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}} \end{align*}\]

On remarque que:

$\begin{align*} \boxed{t \in [0;\pi]} \end{align*}$ pour $T_n$
$\begin{align*} \boxed{t \in ]0;\pi[} \end{align*}$ pour $U_n$

Cette remarque sera utile dans des questions suivantes!!

4 - Montrer que $T'_n(x) = nU_n(x)$

On sait : $ \begin{align*} \begin{cases} \cos(nt) = T_n(\cos t) \\ \sin (nt) = \sin{t} .U_n(\cos t) \end{cases} \end{align*}$

Dérivons $cos(nt)$ de 2 façons différentes:

$ \begin{align*} \big(cos(nt) \big)' = -n.sin(nt) = -n.sint.U_n(cost) = -sint.\underbrace{n.U_n(cost)} \end{align*}$
$ \begin{align*} \big(cos(nt) \big)' = \big[ T_n(cost) \big] '= -sint.\underbrace{T'_n(cost)} \end{align*}$

Par identification, il vient:
$n.U_n(cost) = T'_n(cost) \Leftrightarrow T'_n(x) = n.U_n(x)$

Les fonctions polynômiales $T'_n$ et $n.U_n$ coïncident sur un ensemble infini, en l'occurrence l'ensemble des $cos t$, $t \in \mathbb R - k\pi \space (k \in \mathbb Z)$, donc ces 2 polynômes sont égaux. (voir la démonstration en question 2 pour l'unicité de $T_n$ et $U_n$ )

\[T'_n(X) = n.U_n(X)\]

5 - Relation entre $T_{n+1}$, $T_{n}$, $T_{n-1}$

Il existe plusieurs façons de poser le problème et d'y répondre:

trouver une relation entre $T_{n+1}$, $T_{n}$, $T_{n-1}$. C'est au candidat de trouver cette relation.
Démontrer que $\begin{align*} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}$ par calcul direct

1 - trouver une relation entre $T_{n+1}$, $T_{n}$, $T_{n-1}$. C'est au candidat de trouver cette relation.

Pour cela nous allons utiliser: $ cosa.cosb =\frac{1}{2}(cos(a+b)+ cos(a-b))$

Calculons: $cos(nt)cost$de façon apparaitre du $(n+1)$ et du $(n-1)$
$\begin{align*} cos(nt).cost & = \frac{1}{2} \big[ cos(nt+t) + cos(nt-t)\big] \\
& = \frac{1}{2} \big [cos[(n+1)t]+ cos[(n-1)t] \big] \\ \end{align*}$

Et comme $cos(nt)=T_n(cost)$:
$\begin{align*} \Leftrightarrow & T_n(cost).cost = \frac{1}{2} \big[ T_{n+1}(cost)+ T_{n-1}(cost)] \big] \\
\Leftrightarrow & 2T_n(cost).cost = T_{n+1}(cost)+ T_{n-1}(cost)\\ \end{align*}$

En remplaçant $cost$ par X (voir la question 2):
$\begin{align*} \Leftrightarrow & 2T_n(X).X = T_{n+1}(X)+ T_{n-1}(X) \\
\Leftrightarrow & 2X.T_n(X) = T_{n+1}(X)+ T_{n-1}(X) \\
\Leftrightarrow & T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}$

Pour l'unicité, on procède comme dans la question 2 avec:
$\begin{align*}T_{n+1}(X)+ T_{n-1}(X) - 2X.T_n(X) = 0 \end{align*}$

Si $T_{n-1}$ et $T_{n}$ sont des polynômes , alors $T_{n+1}$ est aussi un polynôme. On peut le démontrer par récurrence simple et triviale. Cela a aussi été démontré dans la question 2.

\[\begin{align*} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}\]

2 - Démontrer que $\begin{align} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align}$ par calcul direct

On sait : $cosa+cosb= 2 cos(\frac{a+b}{2})cos(\frac{a-b}{2})$

calcul de: $T_{n+1}(X)+T_{n-1}(X)$
$\begin{align*} T_{n+1}(X)+T_{n-1}(X) & = cos[(n+1)t]+ cos[(n-1)t] \\
& = 2 cos \bigg[\frac{(n+1)t + (n-1)t}{2} \bigg] cos \bigg [\frac{(n+1)t-(n-1)t}{2} \bigg] \\
& = 2cos(nt).cost \\ & = 2.cost.cos(nt) \\ & = 2XT_n(X)\end{align*}$

Si $T_{n-1}$ et $T_{n}$ sont des polynômes , alors $T_{n+1}$ est aussi un polynôme. On peut le démontrer par récurrence simple et triviale. Cela a aussi été démontré dans la question 2.

Si $t \in \mathbb R$, alors $X \in [-1;1]$

\[\begin{align*} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}\]

6 - En déduire les degré et coefficient dominant de $T_n$

Démonstrations par récurrence:

1 - le degré de $T_n$ et de $U_n$

On connait: $\begin{align*} \begin{cases} T_0=1 \\ T_1=X \\ T_2=2x^2-1 \end{cases} \text{ et: } \begin{cases} \forall X \in [-1;1], \space & T_{n+1}(X) = 2X.T_n(X)- T_{n-1}(X) \\ \Leftrightarrow & T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{cases}\end{align*}$

Soit la proposition $P_n$: $deg(T_n)=n$

Initialisation:
Par calcul : $\begin{align*}\begin{cases} deg(T_0)=deg(1)=0 \\ deg(T_1)=deg(X) = 1 \end{cases} \end{align*}$
Par hypothèse:$\begin{align*}\begin{cases} deg(T_0) =0 \\ deg(T_1) =1 \end{cases} \end{align*}$
$P_n$ est vrai aux rangs $(n=0)$, et $(n=1)$
Récurrence:
Considérons la proposition $P_n$ : $ deg(T_n)=n$ vraie aux rangs $n$ et $n+1$
Et montrons que $P_{n+2}$ est vraie, soit $deg(T_{n+2})=n+2$
$\begin{align*}T_{n+2}(X) & = 2X.T_{n+1}(X)- T_n(X) \end{align*}$
$\begin{align*} deg( T_{n+2}(X)) & = deg(2X.T_{n+1}(X)- \underbrace{T_n(X)}_{\text{de degré inférieur a }(n+1)} \\ & = deg(2X)+deg(T_{n+1}(X)) \\ & = deg(X)+ deg(T_{n+1}(X)) \\ & = 1+n+1 = n+2 \end{align*}$
Alors $P_n$ est vraie au rang $n+2$
Conclusion:
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$. Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N$

\[ \forall n \in \mathbb N, \space \space \space deg(T_n) = n \]

2 - Le coefficient dominant

On connait: $\begin{align*} \begin{cases} T_0=1 \\ T_1=X \\ T_2=2x^2-1 \\ T_3= 4X^3-3X \end{cases} \text{ et: } \begin{cases} \forall X \in [-1;1], \space & T_{n+1}(X) = 2X.T_n(X)- T_{n-1}(X) \\ \Leftrightarrow & T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{cases}\end{align*}$

On peut remarquer que à chaque itération, le coefficient dominant est multiplié par $2$.
$n=0$: pas d'idée!!
$n=1 : dom(T_1) = 1 = 2^0 $
$n=2: dom(T_2) = 2 = 2^1 $
$n=3: dom(T_3) = 4 = 2^{2}$

Soit la proposition $P_n$: Le coefficient dominant $dom(T_n) = 2^{n-1} $ et $\underline{n \neq 0}$

Initialisation
Par calcul: $\begin{align*}\begin{cases} dom(T_1)=dom(1)=1 \\ dom(T_2)=dom(2X^2-1) = 2 \end{cases} \end{align*}$
Par hypothèse: $\begin{align*}\begin{cases}dom(T_1) = 2^{1-1} = 2^0=1 \\ dom(T_2) = 2^{2-1} = 2^1=2 \end{cases} \end{align*}$
$P_n$ est vrai aux rangs $(n=1)$, $(n=2)$
Récurrence:
Considérons la proposition $P_n$ : $ dom(T_{n})=2^{n-1} $ vraie aux rangs $n$ et $n+1$
Et montrons que $P_{n+2}$ est vraie, soit $dom(T_{n+2}) = 2^{(n+2)-1}$
$\begin{align*}dom(T_{n+2}) & = dom(2X.T_{n+1}) \\ & = 2 \times dom(T_{n+1}) \\ & = 2 \times 2^n = 2^{n+1}= 2^{(n+2)-1} \end{align*}$
Alors $P_n$ est vraie au rang $n+2$
Conclusion:
$P_n$ est vrai aux rangs $(n=1)$, $(n=2)$ . Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N^*$

\[ \forall n \in \mathbb N^*, \space \space \space dom(T_n) = 2^{n-1} \]

3 - Confirmation avec la question 2

Question 2 : $T_n(x) = \sum\limits_{k=0}^{ \lfloor n/2 \rfloor} {(-1)}^{k} \binom{n}{2k}x^{n-2k} \space {(1-x^2)}^k$

$\begin{align*} deg \big(T_n(x) \big) & = deg \bigg(\sum\limits_{k=0}^{ \lfloor n/2 \rfloor} {(-1)}^{k} \binom{n}{2k}x^{n-2k} \space {(1-x^2)}^k \bigg)\\
& = deg \bigg((x^{n-2k}) {(1-x^2)}^k \bigg) \\
& = deg(x^{n-2k})+ deg \big( {(1-x^2)}^k) \big) \\
& = n-2k + 2k = n \end{align*}$
On peut remarquer que les $2k$ s'annulent et que $deg \big(T_n(x) \big)$ est indépendant de $k$

Pour le coefficient dominant, on recherche le coefficient correspondant au degré $n$
$\begin{align*} dom \big(T_n(x) \big) & = dom \big(\sum\limits_{k=0}^{ \lfloor n/2 \rfloor} {(-1)}^{k} \binom{n}{2k}x^{n-2k} \space {(1-x^2)}^k \big) = \sum\limits_{k=0}^{ \lfloor n/2 \rfloor} \binom{n}{2k} \end{align*}$
On ne veut garder que les cas pairs. Alors on fait un changement de variable. Il faut changer l'opérande pour cela en $\big(1 + (-1)^k \big)$, ainsi l'opérande est à $0$ pour les cas impairs et a $2$ pour les cas pairs.
$\begin{align*} dom \big(T_n(x) \big) & = \frac{1}{2}\sum\limits_{k=0}^{ n} \binom{n}{k} \big(1 + (-1)^k \big) \\
& = \frac{1}{2} \underbrace{\sum\limits_{k=0}^{ n} \binom{n}{k}}_{(1+1)^n=2^n} + \frac{1}{2} \underbrace{\sum\limits_{k=0}^{ n} \binom{n}{k} (-1)^k}_{(1-1)^n=0^n} \\
& = \frac{1}{2}2^{n}+ \frac{0^n}{2} =2^{n-1}+0= 2^{n-1} \end{align*}$

7 - Montrer que $T_n$ a la même parité que $n$

Soit la proposition $P_n$: "$T_n $ a la même parité que $n$", qui peut aussi s'écrire $\boxed{T_n(-X) = (-1)^nT_n(X)}$, ainsi:
si n est pair, $(-1)^n = 1$ et $T_n(-X) = T_n(X)$
si n est impair, $(-1)^n = -1$ et $T_n(-X) = -T_n(X)$

Initialisation
Par calcul : $\begin{align*}\begin{cases} \begin{cases} (T_0)(X) = 1\\ (T_0)(-X)=1 \end{cases} \Rightarrow 0 \text{ et } T_0 \text{ ont la même parité} \\ \begin{cases} (T_1)(X) = X\\ (T_1)(-X)=-X \end{cases} \Rightarrow 1 \text{ et } T_1 \text{ ont la même parité} \end{cases} \end{align*}$
Par hypothèse: $\begin{align*}\begin{cases} n=0 \text{ est pair donc } T_0 \text{ est pair} \\ n=1 \text{ est impair donc }T_1 \text{ est pair} \end{cases} \end{align*}$
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$
Récurrence:
Considérons la proposition $P_n$ : "$T_n $ a la même parité que $n$" ou encore $T_n(-X) =(-1)^n T_n(X)$ vraie aux rangs $n$ et $n+1$
Et montrons que $P_{n+2}$ est vraie, soit "$T_{n+2} $ a la même parité que $n+2$" ou encore la même parité que $n$
$\begin{align*}T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{align*}$
$\begin{align*}T_{n+2}(-X) & = 2(-X).T_{n+1}(-X)- T_n(-X) \\
& = 2(-X)(-1)^{n+1}T_{n+1}(X)-(-1)^{n}T_n(X) \\
& = (-1)^{n+2}2X T_{n+1}(X) - (-1)^{n}T_n(X) \\
& = (-1)^{n} \times 1^2 \times 2X T_{n+1}(X) - (-1)^{n}T_n(X) \\
& = (-1)^{n} 2X T_{n+1}(X) - (-1)^{n}T_n(X) \\
& = (-1)^{n} \big[ 2X T_{n+1}(X) - T_n(X)\big] \\
& = (-1)^{n} T_{n+2}(X) \end{align*}$
$T_{n+2}$ a la même parité que $n$, donc la même parité que $n+2$
Alors $P_{n+2}$ est vraie
Conclusion:
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$. Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N$

\[ \forall n \in \mathbb N \space \space \space T_n \text{ a la parité de }n\\ T_n(-X)=(-1)^n T_n(X) \]

8 - Montrer que $\forall n \in \mathbb N$, $T_n(1) = 1 $ , $T'_n(1) = n^2$ , $T_n(0)=0$ si $n$ est pair, $T_n(0) =(-1)^{n/2}$ sinon .

1 - $\forall n \in \mathbb N$, $T_n(1)=1$

Soit la proposition $P_n$: $T_n(1)=1 $

Initialisation:
Par calcul : $\begin{align*} \begin{cases}T_0(1) = 1 \\ T_1(1) = 1 \end{cases} \end{align*} $
Par hypothèse : $\begin{align*} \begin{cases}T_0(1) = 1 \\ T_1(1)=1 \end{cases} \end{align*}$
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$
Récurrence::
Supposons $P_n$ : $T_n(1)=1 $
Et montrons que $P_{n+2}$ est vraie, soit $T_{n+2}(1)=1 $
$\begin{align*}T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{align*}$
$\begin{align*} T_{n+2}(1) & = 2 \times 1 \times T_{n+1}(1)- T_n(1) \\
& = 2 \times 1 \times 1-1 = 1 \end{align*}$
Alors $P_n$ est vraie au rang $n+2$
Conclusion:
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$. Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N$

\[ \begin{align*} \forall n \in \mathbb N, \space \space T_n(1)=1 \end{align*} \]

2 - $\forall n \in \mathbb N$, $T'_n(1)=n^2$

$T_n$ est un polynôme et est de classe $C^\infty$. En particulier elle est dérivable.

On connait: $\begin{align*} \begin{cases}T_0(X) = 1 \Rightarrow T'_0(X)=0 \\T_1(X) = X \Rightarrow T'_1(X) = 1 \end{cases} \end{align*}$
$\begin{align*} \forall X \in [-1;1], \space \space T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{align*}$

Par récurrence:

Soit la proposition $P_n$: $T'_n(1)=n^2 $

Initialisation:
Par calcul $\begin{align*} \begin{cases} T'_0(1) = 0 \\ T'_1(1) = 1 \end{cases} \end{align*}$
Par hypothèse: $\begin{align*} \begin{cases}T'_0(1) = 0^2=0 \\T'_1(1)=1^2 = 1 \end{cases} \end{align*}$
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$
Récurrence::
Supposons $P_n$ : $T'_n(1)=n^2 $ vraie aux rangs $n$ et $n+1$
Et montrons que $P_{n+2}$ est vraie, soit $T'_{n+2}(1)=(n+2)^2 $
$\begin{align*} T'_{n+2}(X) & =\big [ 2X T_{n+1}(X)- T_n(X) \big]' \\
& = 2 \times T_{n+1}(X) + 2XT'_{n+1}(X) -T'_n(X) \end{align*}$
$\begin{align*}T'_{n+2}(1) & = 2 \times T_{n+1}(1) + 2 \times 1 \times T'_{n+1}(1) -T'_n(1) \\
& = (2 \times 1) + (2 \times (n+1)^2) -n^2 = 2 + 2n^2+4n+2-n^2 \\
& = n^2+4n+4 = (n+2)^2 \end{align*}$
Alors $P_n$ est vraie au rang $n+2$
Conclusion:
$P_n$ est vrai aux rangs $(n=0)$, $(n=1)$. Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N$

\[ \begin{align*} \forall n \in \mathbb N, \space \space T'_n(1)=n^2 \end{align*} \]

3 - Montrer que $T_n(0)=0$ si $n$ est impaire et $T_n(0)=(-1)^{n/2}$ sinon

Si $n$ est impair:
Si $n$ est impair , alors $T_{n}$ est impair (Question 7)
Les $T_n$ impairs sont symétriques par rapport au centre du repère $O$ et passe par le centre du repère.
En conséquence, $T_{n}(0) = 0$ et cela pour tout $n \text{ impair } \in \mathbb N$
Si $n$ est pair: alors $n=2k$
Soit la proposition $P_{n}$ : "si $n$ est pair alors $P_{n}(0) = (-1)^{n/2}$ "
- Initialisation
  par calcul : $\begin{align*} \begin{cases} T_0(0)=1 \\ T_2(0) =2 \times 0^2 -1 = -1 \end{cases} \end{align*}$
  par hypothèse: $\begin{align*} \begin{cases} T_0(0) = (-1)^{0/2} = 1 \\ T_2(0) = (-1)^{2/2} = -1 \end{cases} \end{align*}$
  $P_{n}$ est vraie aux rangs $(n=0)$, $(n=2)$
- Récurrence:
  Considérons $P_{n}$ : $T_{n} = (-1)^{n/2}$ vraie aux rangs $n$ , et $T_{n+1}(0)=0$
  Montrons que $T_{n+2}(X) = (-1)^{(n+2)/2}$
  $\begin{align*}T_{n+2}(X) & = 2X.T_{n+1}(X)- T_n(X) \end{align*}$ avec $n=2k$
  $\begin{align*} T_{n+2}(X) & = T_{2k+2}(X) = 2X.\cancel{T_{2k+1}(X)}^{=0}- T_{2k}(X) \\
  & = 2X \times 0 - T_{2k}(X) \\
  & = - (-1)^{k} = (-1)^{k+1} = (-1)^{(2k+2)/2} = (-1)^{(n+2)/2} \end{align*}$
  Alors $P_n$ est vraie au rang $n+2$
- Conclusion:
  $P_n$ est vrai aux rangs $(n=0)$, et $(n=2)$ . Par récurrence, si elle est vraie aux rangs $n$ et $n+1$, alors elle est vraie au rang $n+2$. $P_n$ est donc vraie pour tout $n \in \mathbb N$
  
  \[ \begin{align*} T_n(0) = 0 \text{ si n est impair} \\ T_n(0) = (-1)^{n/2} \text{ si n est pair} \end{align*} \]

$T_{n} (0) = 0$

9 - Montrer que pour $n \in \mathbb N^$, $T_n$ possède $n$ racines simples $\begin{align}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align}$ et que $\begin{align} \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}$

Il s 'agit de trouver ici les racines du polynôme $T_n(x)$
$\begin{align*}\Leftrightarrow & \exists ? x \in \mathbb R \space \space / \space \space T_n(x) = 0 \\
\Leftrightarrow & \exists ? t \in \mathbb R \space \space / \space \space T_n(cost) = 0 \\ \Leftrightarrow & \exists ? t \in \mathbb R \space \space / \space \space cos(nt) = 0\end{align*}$

On pose:
$x= cost \Rightarrow x \in [-1;1]$, et dans ce cas , $ t = arccos(x) \Rightarrow \underline{t \in [0;\pi]}$

$ \begin{align*}T_n(cost) & = 0 \Leftrightarrow cos(nt) =0 \\
& \Rightarrow nt = \frac{\pi}{2} + k \pi, \space k \in \mathbb Z \\ & \Leftrightarrow t =\frac{\pi}{2n}+\frac{k \pi}{n} , \space k \in \mathbb Z , \space \space \underline{\forall n \in \mathbb N^*} \end{align*}$

pour $k=0$, on a: $t=\frac{\pi}{2n} , \space \space \text{ et } \forall n \in \mathbb N^*, \space 0 \leq \frac{\pi}{2n} \leq \pi$
pour $k=n$, on a: $t =\frac{\pi}{2n}+\frac{n \pi}{n} = \frac{\pi}{2n}+\frac{2n \pi}{2n} = \frac{(2n+1) \pi}{2n} \space \space \text{ et } \forall n \in \mathbb N^*, \space t= \frac{\pi}{2n} \geq \pi$

Il convient alors de retirer de l'ensemble des solutions tous les $k \gt n$, ainsi on aura toujours $0 \leq t \leq \pi $

Posons: $t_k =\frac{\pi}{2n}+\frac{k \pi}{n}$ pour lesquels $cos(nt_k)=0$. Alors la famille $\big( t_k \big)_{k \in [\![ 0;n-1]\!] }$ contient exactement $n$ éléments différents 2 à 2.
La fonction $ x \mapsto cos(x)$ est strictement monotone (décroissante) sur $[0;\pi]$. elle réalise alors une bijection sur $[0;\pi]$.
Posons: $x_k = cos(t_k)$ tel que $T_n(x_k) = 0$. Alors, la famille $\big( x_k \big)_{k \in [\![ 0;n-1]\!] }$ contient elle aussi exactement $n$ élément sur $[-1;1]$ différents 2 à 2.

$T_n$ est un polynôme de degré $n$
La famille $\big( x_k \big)_{k \in [\![ 0;n-1]\!] }$ contient $n$ éléments différents 2 à 2 tels que $T_n(x_k) = 0$.
Nous avons donc trouvé les n racines simples (racines différentes 2 à 2) du polynôme $T_n$ de degré $n$.

En conséquence , le polynôme $T_n$ possède $n$ racines simples $x_k = cos(t_k)$ avec $x_k \in [-1;1]$ et $k \in [\![ 0;n-1]\!]$

$ \forall n \in \mathbb N^*$, $T_n$ possède $n$ racines simples $\begin{align*}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align*}$

Si un polynôme $P$ de degré $n$ et de coefficient dominant $a_n$ possède $n$ racines simples $x_i$ , alors on peut le mettre sous la forme $P = a_n \prod\limits_{i=0}^{n}(X-x_i)$
Dans notre cas , $dom(T_n) = 2^{n-1}$

\[\begin{align*} \forall n \in \mathbb N^*, \space T_n(X) = 2^{n-1} \prod\limits_{k=0}^{n-1} \bigg[ X- cos\big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big) \bigg] \end{align*} \]

Si $n$ est pair, alors $T_n$ est pair , le coefficient du terme en puissance $n-1$ (impair) est nul: $a_{n-1}=0$
Si $n$ est impair, alors $T_n$ est impair , le coefficient du terme en puissance $n-1$ (pair) est nul: $a_{n-1}=0$

Donc $a_{n-1}=0$ dans tout les cas et :

\[\begin{align*} \forall n \in \mathbb N^*, \space \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}\]

$T_{n} (0) = 0$

10 - Trouver les EXTREMA de $T_n$

Par définition: $T_n(x) = T_n(cost) = cos(nt)$

Comme dans la question 9 :

$\begin{align*}\Leftrightarrow & \exists ? x \in \mathbb R \space \space / \space \space T_n(x) \text{ soit maximum} \\
\Leftrightarrow & \exists ? t \in \mathbb R \space \space / T_n(cost)\space \space \text{ soit maximum} \\ \Leftrightarrow & \exists ? t \in \mathbb R \space \space / \space \space cos(nt) \text{ soit maximum}\end{align*}$

On pose:
$x= cost \Rightarrow x \in [-1;1]$, et dans ce cas , $ t = arccos(x) \Rightarrow \underline{t \in [0;\pi]}$
Et finalement: $ \lvert T_n(x) \rvert \leq 1$ et $\exists ? x \in [-1;1] \space \space / \space \space \lvert T_n(x) \rvert = 1$

$ \begin{align*}T_n(cost) \text{ est maximum }& \Leftrightarrow \lvert cos(nt) \rvert =1 \\
& \Rightarrow nt = k \pi, \space k \in \mathbb Z \\ & \Leftrightarrow t =\frac{k \pi}{n} , \space k \in \mathbb Z , \space \space \underline{\forall n \in \mathbb N^*} \end{align*}$

pour $k=0$, on a: $t=0 , \space \space \text{ et } \forall n \in \mathbb N^*, t \in [0;\pi]$
pour $k=n$, on a: $t =\frac{n\pi}{n}= \pi \text{ et } \forall n \in \mathbb N^*, \space t \in [0;\pi]$

Posons: $t'_k =k \pi$ pour lesquels $\lvert cos(nt'_k) \rvert =1$. Alors la famille $\big( t'_k \big)_{k \in [\![ 0;n]\!] }$ contient exactement $n+1$ éléments différents 2 à 2.
La fonction $ x \mapsto cos(x)$ est strictement monotone (décroissante) sur $[0;\pi]$. elle réalise alors une bijection sur $[0;\pi]$.
Posons: $x'_k = cos(t'_k)$ tel que $T_n(x'_k) \text{ soit maximum}$. Alors, la famille $\big( x'_k \big)_{k \in [\![ 0;n]\!] }$ contient elle aussi exactement $n+1$ élément sur $[-1;1]$ différents 2 à 2.

Nous avons donc trouvé les $n+1$ extrema (différents 2 à 2) du polynôme $T_n$

$ \forall n \in \mathbb N^*$, $T_n$ possède $n+1$ extrema, en $\begin{align*}x'_k = cos \big(\frac{k \pi}{n}\big)_{0 \leq k \leq n} \space , \space x_k \in [-1;1] \end{align*}$

11 - Montrer que $ \begin{align} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align}$

$\begin{align*} \forall n \in \mathbb N^*, \space T_n(X) = 2^{n-1} \prod\limits_{k=0}^{n-1} \bigg[ X- cos\big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big) \bigg] \end{align*} $

$ \begin{align*}T_n(0) & = a_0 = 2^{n-1} \prod\limits_{k=0}^{n-1} \bigg[ 0- cos\big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big) \bigg] \\ & = 2^{n-1} (-1)^n\prod\limits_{k=0}^{n-1} x_k \end{align*} $

Si $n$ est impair, alors $a_0 = 0$ car $T_n(0) = 0$ (question 8). Et alors $\prod\limits_{k=0}^{n-1}x_k = 0$
si $n$ est pair, alors $a_0=(-1)^{n/2}$ (question 8) et alors $(-1)^{n/2} = 2^{n-1} \underbrace{(-1)^n}_{=1}\prod\limits_{k=0}^{n-1} x_k$ .
Et en conséquence: $\prod\limits_{k=0}^{n-1} x_k = \frac{(-1)^{n/2}}{2^{n-1}}$

\[ \begin{align*} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align*}\]

12 - Montrer que $T_n$ est solution de l'équation différentielle: $(E): (X^2-1)y" + Xy' - n^2y=0$

$T_n$ est solution de (E) $\Leftrightarrow (X^2-1)T"_n + XT'_n - n^2T_n=0$

On a: $cos(nt) = T_n(cost)$
$T_n$ est un polynôme, il est donc de clace $C^\infty$

En dérivant des 2 côtés une première fois, il vient:
$-n.sin(nt) = -sint.T'_n(cost)$

En dérivant une seconde fois, il vient:
$\begin{align*} & -n^2cos(nt) = -cost.T'_n(cost)- sint.(-sint).T^{"}_n(cost) \\
\Rightarrow & -n^2T_n(cost) = -cost.T'_n(cost)+ sin^2t.T^{"}_n(cost) \\
\Rightarrow & -n^2T_n(cost) = -cost.T'_n(cost)+ (1-cos^2t).T^{"}_n(cost) \\
\Rightarrow & (cos^2t-1)T^{"}_n(cost) + cost.T'_n(cost) -n^2T_n(cost) = 0, \space \forall t \in \mathbb R \\
\forall X \in & [-1;1] , \space \exists!t \in [0;\pi], \space \space X=cost \\
\Rightarrow & (X^2-1)T^{"}_n(X) + X.T'_n(X) -n^2T_n(X) = 0, \space \forall X \in [-1;1] \end{align*}$

Nous avons un polynôme qui est nul pour une infinité de valeurs de $[-1;1]$. C 'est donc le polynôme identiquement nul. Et en conséquence, ce polynôme est nul quelque soit $X \in \mathbb R$ et ( idem question 2 sur l 'unicité de $T_n$) :
$(X^2-1)T^{"}_n(X) + X.T'_n(X) -n^2T_n(X) = 0, \space \forall X \in \mathbb R $
Donc $T_n$ est bien solution de (E)

\[\begin{align*}(X^2-1)T^{"}_n(X) + X.T'_n(X) -n^2T_n(X) = 0, \space \forall X \in \mathbb R \\ T_n \text{est solution de } (E): (X^2-1)y" + Xy' - n^2y=0 \end{align*}\]

13 - Soit $E$ le $\mathbb R$-espace vectoriel des fonctions continues de $[-1;1]$ dans $\mathbb R$. Justifier que l'application de $E^2 \to \mathbb R$ définie par $\langle f(t),g(t) \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt$ est un produit scalaire.

1 - Existence de $\begin{align} \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt = I \end{align}$

Soient $f$ et $g$, 2 fonctions continues sur $]-1;1[$ et $(f,g) \in E^2$. Alors le produit des fonctions $fg$ est continue sur $]-1;1[$ .

$\begin{align*} I & = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt \\
& = \int_{-1}^{0}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt + \int_{0}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt \end{align*}$

Comme $fg$ est continue sur un segment, par théorème des valeurs extrêmes, il existe un majorant $M$ de $\lvert f(t)g(t) \rvert$ et

$\begin{align*} \forall t \in \mathbb R, \space \Bigg| \frac{f(t)g(t)}{\sqrt{1-t^2}} \Bigg| \leq \frac{M}{\sqrt{(1-t)(1+t)}} \end{align*}$

Au voisinage de $t=1$:
$\begin{align*} \frac{M}{\sqrt{(1-t)(1+t)}} \underset{t \to 1}{\sim} \frac{M}{(1-t)^{1/2} \sqrt{2}} \end{align*}$
Et d'après le critère de Riemman ($\begin{align*} \int_0^1\frac{dt}{t^{\alpha}} \text{ converge} \Longleftrightarrow \alpha=1/2 \lt 1 \end{align*}$ ) $\begin{align*}\int_{0}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt \end{align*}$ converge.
Au voisinage de $t=-1$:
$\begin{align*} \frac{M}{\sqrt{(1-t)(1+t)}} \underset{t \to -1}{\sim} \frac{M}{(1+t)^{1/2} \sqrt{2}} \end{align*}$
Et d'après le critère de Riemman ($\begin{align*} \int_{-1}^0 \frac{dt}{t^{\alpha}} \text{ converge} \Longleftrightarrow \alpha=1/2 \lt 1 \end{align*}$ ) $\begin{align*}\int_{-1}^{0}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt \end{align*}$ converge.
Conclusion:
la fonction $t \mapsto \frac{f(t)g(t)}{\sqrt{1-t^2}}$ est bien intégrable sur $]-1;1[$, l'intégrale $I=\int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt$ converge, la fonction $\langle f,g \rangle$ est bien définie.

2 - $\langle f,g \rangle$ est il un produit scalaire?

Un produit scalaire est une forme bilinéaire symétrique et définie positive

forme symétrique: $\langle f,g \rangle = \langle g,f \rangle$ ?
On l 'obtiendra par la symétrie de l'intégrale: $ \int f \times g = \int g \times f$
Soient $(f,g) \in E^2$
$\begin{align*} \langle f,g \rangle & = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt
= \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt
= \langle g,f \rangle \end{align*}$
forme bilinéaire
- Par rapport à la première variable: $ \langle \lambda f + \mu g , h \rangle = \lambda \langle f , h \rangle + \mu \langle g , h \rangle$ ?
  Soient $(f,g,h) \in E^3$ et $(\lambda , \mu ) \in \mathbb R^2$
  $\begin{align*} \langle \lambda f + \mu g , h \rangle & = \int_{-1}^{1}\frac{(\lambda f + \mu g)(t)h(t) }{\sqrt{1-t^2}}dt
  = \int_{-1}^{1}\frac{((\lambda f)(t) + (\mu g)(t))(h(t)) }{\sqrt{1-t^2}}dt \\
  & = \int_{-1}^{1}\frac{(\lambda f(t) + \mu g(t))(h(t)) }{\sqrt{1-t^2}}dt
  = \int_{-1}^{1}\frac{\lambda f(t)h(t) }{\sqrt{1-t^2}}dt + \int_{-1}^{1}\frac{ \mu g(t)h(t) }{\sqrt{1-t^2}}dt \\
  & = \lambda \int_{-1}^{1} \frac{ f(t)h(t) }{\sqrt{1-t^2}}dt+ \mu \int_{-1}^{1} \frac{ g(t)h(t) }{\sqrt{1-t^2}}dt
  =\lambda \langle f , h \rangle + \mu \langle g , h \rangle \end{align*}$
- Par rapport à la première variable: La 2ème linéarité est obtenue par symétrie, déjà démontrée.
forme définie positive: $ \langle f,f \rangle \geq 0 $ ? et $ \langle f,f \rangle =0 \Leftrightarrow f = 0 $
Soit $f \in E$
- Positive : $\langle f , f \rangle \geq0$ ?
  $\begin{align*} \langle f,f \rangle = \int_{-1}^{1}\frac{f(t)f(t)}{\sqrt{1-t^2}}dt = \int_{-1}^{1}\frac{\overbrace{f^2(t)}^{\geq 0}}{\underbrace{\sqrt{1-t^2}}_{\gt 0}}dt \geq 0 \end{align*}$ par positivité de l'intégrale d'une fonction positive.
- Définie postive: $\langle f,f \rangle =0 \Longleftrightarrow f=0$
  Si $\int_{-1}^{1}\frac{\overbrace{f^2(t)}^{\geq 0}}{\underbrace{\sqrt{1-t^2}}_{\gt 0}}dt = 0$ alors $f(t) = 0 \space \forall t \in [-1;1]$. Donc f(t) est le polynôme identiquement nul et $\forall t \in \mathbb R, \space f(t) = 0$
  De même , si $f=0$ alors on aura $\langle f,f \rangle =0$
  Et pour finir , $\langle f,f \rangle =0 \Longleftrightarrow f=0$

\[\langle f,f \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt\] définit bien un produit scalaire sur $E$

14 - Pour tous $(m,n) \in \mathbb N^2$, calculer le produit scalaire $\langle T_n , T_m \rangle$. Que peut on dire de la famille $\big(T_n\big)_{n \in \mathbb N}$ ?

$\begin{align*} \langle T_n , T_m \rangle & = \int_{-1}^{1} \frac{T_n(x) T_m(x)}{\sqrt{1-x^2}} dx \end{align*}$ et $T_n(cost) = cos(nt)$

Procédons à un changement de variable:
$\begin{align*} \begin{cases} x= cost \\ dx = -sint.dt \end{cases} \Rightarrow \begin{cases} t \xrightarrow{x \to 1} 0 \\ t \xrightarrow{x \to -1} \pi \end{cases} \text{ et } \begin{cases} t = arcos (x) , x \in ]-1;1[ \\ t \in ]0;\pi[ \text{ et } sint \gt 0 [\end{cases} \end{align*}$

$\begin{align*} \langle T_n , T_m \rangle & = \int_{x=-1}^{x=1} \frac{T_n(x) T_m(x)}{\sqrt{1-x^2}} dx
= \int_{t=\pi}^{t=0} \frac{T_n(cost) T_m(cost)}{\sqrt{1-cos^2t}} (-sint)dt \\
& = \int_{t=0}^{t=\pi} \frac{T_n(cost) T_m(cost)}{\sqrt{sin^2t}} sint.dt = \int_{t=0}^{t=\pi} \frac{cos(nt) (cost(m)}{sint} sint.dt \\
& = \int_{t=0}^{t=\pi} cos(nt) (cos(mt) dt = \int_{t=0}^{t=\pi} \frac{1}{2} \big[ cos \big( (m+n)t \big) +cos \big( (m-n)t \big) \big]dt \end{align*}$

Si $ n=m=0$
$\begin{align*} \langle T_n , T_m \rangle & = \int_{t=0}^{t=\pi} \frac{1}{2} \big[ cos \big( (m+n)t \big) +cos \big( (m-n)t \big) \big]dt \\ & = \frac{1}{2} \int_{t=0}^{t=\pi} (1+1)dt =\int_{t=0}^{t=\pi} (1+1)dt = \pi \end{align*}$
Si $n = m \neq 0$
$\begin{align*} \langle T_n , T_m \rangle & = \int_{t=0}^{t=\pi} \frac{1}{2} \big[ cos \big( (m+n)t \big) +cos \big( (m-n)t \big) \big]dt \\ & = \frac{1}{2} \int_{t=0}^{t=\pi} (cos(2nt)+1)dt =\frac{1}{2} \bigg[ \frac{sin(2nt)}{2n} + t \bigg]_0^\pi = \pi/2 \end{align*}$
Si $n \neq m 0$
$\begin{align*} \langle T_n , T_m \rangle & = \int_{t=0}^{t=\pi} \frac{1}{2} \big[ cos \big( (m+n)t \big) +cos \big( (m-n)t \big) \big]dt \\ & =\frac{1}{2} \bigg[ \frac{sin\big( (m+n)t \big)}{m+n} + \frac{sin\big( (m-n)t \big)}{m-n} \bigg]_0^\pi = 0 \end{align*}$

Si $m \neq m$, alors la famille $ \langle T_n , T_m \rangle = 0$ , alors $\bigg(T_n \bigg)_{n \in \mathbb N}$ est une famille orthogonale de $\mathbb R[X]$ au sens de $\langle . , . \rangle$. La famille $ \langle T_n , T_m \rangle = 0$ , alors $\bigg(T_n \bigg)_{n \in \mathbb N}$ n 'est pas normée.

\[\begin{align*} \forall (n,m) \in \mathbb N^2, \space \langle T_n , T_m \rangle = \begin{cases} \pi \text{ si } n=m=0\\ \pi/2 \text{ si } n=m \neq 0 \\ 0 \text{ si } n \neq 0 \end{cases} \end{align*} \] \[ \bigg(T_n \bigg)_{n \in \mathbb N} \text{ est une famille othogonale de } \mathbb R[X]\]

15 - A partir du résultat de la question 4 et des autres résultats, déterminer les degré et coefficient dominant de $U_n$

Résultat de la question 4 : $T'_n(X) = n.U_n(X)$ et donc $U_n(X) =\frac{1}{n} T'_n(X)$
Si $T_n = a_nx^n + \cdots + a_0 $, alors $T'_n = n.a_nx^{n-1} + \cdots \cdots$

$deg(U_n)$
$deg(U_n) = deg (\frac{1}{n} T'_n) =deg ( T'_n)$
avec $deg(T_n) = n \Rightarrow deg(T'_n)=n-1$
$deg(U_n) = n-1$ avec $n\geq 1$
On vérifie avec: $\begin{align*} \begin{cases} & U_1=1 && U_2=2X && U_3=4X^2-1 \\
& deg(U_1)=1-1=0 && deg(U_2)=2-1=1 && deg(U_3)=3-1=2 \end{cases} \end{align*}$
$dom(U_n)$
$dom(U_n) =dom (\frac{1}{n} T'_n) $
avec : $dom(T_n) = 2^{n-1} \Rightarrow dom(T'n)= n \times 2^{n-1}$
$dom(U_n) = dom(\frac{1}{n} T'_n) = \frac{1}{n} \times n \times 2^{n-1} = 2^{n-1}$ avec $n\geq 1$
On vérifie avec: $\begin{align*} \begin{cases} & U_1=1 && U_2=2X && U_3=4X^2-1 \\
& dom(U_1)=2^{1-1}=1 && dom(U_2)=2^{2-1}=2 && dom(U_3)=2^{3-1}=4 \end{cases} \end{align*}$

\[\forall n \in \mathbb N^*, \space deg(U_n) = n-1 \space \space \space \text{ et } \space \space \space dom(U_n) = 2^{n-1} \]

16 - Montrer que $\forall n \in \mathbb N, \exists t \in \mathbb R, \space U_n(cos t) = \frac{sin[(n+1)t]}{sint}$

Dans la question 4 , on a démontré que $T'_n=nU_n$ ou encore $U_n = \frac{1}{n}T'_n$

On sait que $ T_n$ et $cost$ sont de classe $C^\infty$ et que $T_n(cost) = cos(nt)$

En dérivant $cos[(n+1)t]$: $ \big[ cos[(n+1)t] \big]' = -(n+1).sin[(n+1)t]$

En dérivant $T_{n+1}(cost)$: $ \big[ T_{n+1}(cost) \big]' = -sint. T'_{n+1}(cost) $

Avec $ t \neq k \pi, \space k \in \mathbb Z$, il vient:
$\begin{align*}-(n+1).sin[(n+1)t] = -sint T'_{n+1}(cost) & \Leftrightarrow \frac{T'_{n+1}(cost)}{n+1} = \frac{sin[(n+1)t]}{sint} \\ & \Leftrightarrow U_{n+1} = \frac{sin[(n+1)t]}{sint} \end{align*}$

\[\forall n \in \mathbb N, \space \forall t \in \mathbb R/ \pi \mathbb Z, \space U_{n+1}(cost) = \frac{sin[(n+1)t]}{sint} \]

17 - En déduire que $\big( U_n \big)_{n \in \mathbb N}$ suit aussi la relation de récurrence de la question 5, que $ \forall n \in \mathbb N, \space \space U_n$ est scindé simple sur $\mathbb R$, à racine dans $]-1;1[$, en précisant les racines

Soient $n \in \mathbb N$ et $t \in \mathbb R / \pi \mathbb Z$

On a: $sin(a+b) +sin(a-b) = 2sina.cosb \Leftrightarrow sin(a+b) = 2sina.cosb - sin(a-b) $

On a d 'après la question 15:
$\begin{align*} U_{n+2}(cost) & = \frac{sin[(n+2)t]}{sint} = \frac{sin[(n+1)t+t]}{sint} \\
& = \frac{2sin[(n+1)t].cost - sin[(n+1)t-t] }{sint} \\
& = \frac{2sin[(n+1)t].cost - sin(nt) }{sint} \\
& = 2cost \Bigg(\frac{sin[(n+1)t]}{sint} \Bigg) - \frac{sin(nt)}{sint} \\
& = 2cost U_{n+1} -U_n \\
& \Rightarrow U_{n+2}(X) = 2XU_{n+1}(X) - U_n(X) \\
& \Rightarrow U_{n+2}(X) + U_n(X) = 2XU_{n+1}(X) \end{align*}$

Tout comme l'unicité des polynômes $\big( T_n)_{n \in \mathbb N}$ vue à la question 2 , les polynômes $\big( U_n)_{n \in \mathbb N}$ sont eux aussi uniques.

\[ \forall n \in \mathbb N, \space U_{n+2}(X)+U_n(X) = 2XU_{n+1}\]

si $t \in \mathbb R$, $U_n(cost) = 0 \Rightarrow sin[(n+1)t]= 0 \Rightarrow (n+1)t = k \pi \Rightarrow t = \frac{k \pi}{n+1}$

$\forall k \in [\![ 1;n]\!] , \space \alpha_k = \frac{k \pi}{n+1}$ sont au nombre de $n$ et sont distinctes. L'application $cos$ est injective de $]-1;1[$ vers $]0;\pi[$, donc les $cos(\alpha_k)$ sont distincts, et ce sont les racines de $U_n$

Or , la relation : $\forall n \in \mathbb N, \space U_{n+1} = \frac{1}{n+1}T'_{n+1}$non montre que $deg(U_{n+1}) = deg(T'_{n+1}) = n, donc possède n racines, ce qui montre que $U_n$ est scindé simple.

Les polynômes de Tchebychev

Sujet

1 - Donner les expression de \(T_0\), \(T_1\), \(T_2\), \(T_3\), \(U_1\),\(U_2\), \(U_3\)

1 - Existence:

2 - Unicité

3 - Conclusion :

3 - Montrer que \(\forall x \in [-1;1]\), \(T_n(x) = cos(n.arccos(x))\) et \(\forall x \in ]-1;1[\), \(U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}}\)

4 - Montrer que \(T'_n(x) = nU_n(x)\)

5 - Relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\)

1 - trouver une relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\). C'est au candidat de trouver cette relation.

2 - Démontrer que \(\begin{align} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align}\) par calcul direct

6 - En déduire les degré et coefficient dominant de \(T_n\)

1 - le degré de \(T_n\) et de \(U_n\)

2 - Le coefficient dominant

3 - Confirmation avec la question 2

7 - Montrer que \(T_n\) a la même parité que \(n\)

8 - Montrer que \(\forall n \in \mathbb N\), \(T_n(1) = 1 \) , \(T'_n(1) = n^2\) , \(T_n(0)=0\) si \(n\) est pair, \(T_n(0) =(-1)^{n/2}\) sinon .

1 - \(\forall n \in \mathbb N\), \(T_n(1)=1\)

2 - \(\forall n \in \mathbb N\), \(T'_n(1)=n^2\)

3 - Montrer que \(T_n(0)=0\) si \(n\) est impaire et \(T_n(0)=(-1)^{n/2}\) sinon

9 - Montrer que pour \(n \in \mathbb N^\), \(T_n\) possède \(n\) racines simples \(\begin{align}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align}\) et que \(\begin{align} \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}\)

10 - Trouver les EXTREMA de \(T_n\)

11 - Montrer que \( \begin{align} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align}\)

12 - Montrer que \(T_n\) est solution de l'équation différentielle: \((E): (X^2-1)y" + Xy' - n^2y=0\)

13 - Soit \(E\) le \(\mathbb R\)-espace vectoriel des fonctions continues de \([-1;1]\) dans \(\mathbb R\). Justifier que l'application de \(E^2 \to \mathbb R\) définie par \(\langle f(t),g(t) \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt\) est un produit scalaire.

1 - Existence de \(\begin{align} \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt = I \end{align}\)

2 - \(\langle f,g \rangle\) est il un produit scalaire?

14 - Pour tous \((m,n) \in \mathbb N^2\), calculer le produit scalaire \(\langle T_n , T_m \rangle\). Que peut on dire de la famille \(\big(T_n\big)_{n \in \mathbb N}\) ?

15 - A partir du résultat de la question 4 et des autres résultats, déterminer les degré et coefficient dominant de \(U_n\)

16 - Montrer que \(\forall n \in \mathbb N, \exists t \in \mathbb R, \space U_n(cos t) = \frac{sin[(n+1)t]}{sint}\)

17 - En déduire que \(\big( U_n \big)_{n \in \mathbb N}\) suit aussi la relation de récurrence de la question 5, que \( \forall n \in \mathbb N, \space \space U_n\) est scindé simple sur \(\mathbb R\), à racine dans \(]-1;1[\), en précisant les racines

Les polynômes de Tchebychev

Sujet

1 - Donner les expression de \(T_0\), \(T_1\), \(T_2\), \(T_3\), \(U_1\),\(U_2\), \(U_3\)

1 - Existence:

2 - Unicité

3 - Conclusion :

3 - Montrer que \(\forall x \in [-1;1]\), \(T_n(x) = cos(n.arccos(x))\) et \(\forall x \in ]-1;1[\), \(U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}}\)

4 - Montrer que \(T'_n(x) = nU_n(x)\)

5 - Relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\)

1 - trouver une relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\). C'est au candidat de trouver cette relation.

2 - Démontrer que \(\begin{align*} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}\) par calcul direct

6 - En déduire les degré et coefficient dominant de \(T_n\)

1 - le degré de \(T_n\) et de \(U_n\)

2 - Le coefficient dominant

3 - Confirmation avec la question 2

7 - Montrer que \(T_n\) a la même parité que \(n\)

8 - Montrer que \(\forall n \in \mathbb N\), \(T_n(1) = 1 \) , \(T'_n(1) = n^2\) , \(T_n(0)=0\) si \(n\) est pair, \(T_n(0) =(-1)^{n/2}\) sinon .

1 - \(\forall n \in \mathbb N\), \(T_n(1)=1\)

2 - \(\forall n \in \mathbb N\), \(T'_n(1)=n^2\)

3 - Montrer que \(T_n(0)=0\) si \(n\) est impaire et \(T_n(0)=(-1)^{n/2}\) sinon

9 - Montrer que pour \(n \in \mathbb N^*\), \(T_n\) possède \(n\) racines simples \(\begin{align*}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align*}\) et que \(\begin{align*} \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}\)

10 - Trouver les EXTREMA de \(T_n\)

11 - Montrer que \( \begin{align*} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align*}\)

12 - Montrer que \(T_n\) est solution de l'équation différentielle: \((E): (X^2-1)y" + Xy' - n^2y=0\)

13 - Soit \(E\) le \(\mathbb R\)-espace vectoriel des fonctions continues de \([-1;1]\) dans \(\mathbb R\). Justifier que l'application de \(E^2 \to \mathbb R\) définie par \(\langle f(t),g(t) \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt\) est un produit scalaire.

1 - Existence de \(\begin{align*} \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt = I \end{align*}\)

2 - \(\langle f,g \rangle\) est il un produit scalaire?

14 - Pour tous \((m,n) \in \mathbb N^2\), calculer le produit scalaire \(\langle T_n , T_m \rangle\). Que peut on dire de la famille \(\big(T_n\big)_{n \in \mathbb N}\) ?

15 - A partir du résultat de la question 4 et des autres résultats, déterminer les degré et coefficient dominant de \(U_n\)

16 - Montrer que \(\forall n \in \mathbb N, \exists t \in \mathbb R, \space U_n(cos t) = \frac{sin[(n+1)t]}{sint}\)

17 - En déduire que \(\big( U_n \big)_{n \in \mathbb N}\) suit aussi la relation de récurrence de la question 5, que \( \forall n \in \mathbb N, \space \space U_n\) est scindé simple sur \(\mathbb R\), à racine dans \(]-1;1[\), en précisant les racines

2 - Démontrer que \(\begin{align} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align}\) par calcul direct

9 - Montrer que pour \(n \in \mathbb N^\), \(T_n\) possède \(n\) racines simples \(\begin{align}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align}\) et que \(\begin{align} \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}\)

11 - Montrer que \( \begin{align} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align}\)

1 - Existence de \(\begin{align} \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt = I \end{align}\)