Les intégrales de Wallis

Sujet

\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(sint)^n dt\end{align*}\)

Caluler \(I_0\) et \(I_1\)
Montrer que \((I_n)_{n \in \mathbb N}\) est bien définie
Montrer que \(\forall n \in \mathbb N, I_n = \int_0^{\pi/2}(cost)^n dt \) et en déduire \(I_2\)
Montrer que \(I_n\) est convergente
Exprimer \(I_{n+2}\) en fonction de \(I_n\)
Exprimer \(I_{2p}\) et \(I_{2p+1 }\) en fonction de \(p\), \(\forall p \in \mathbb N\)
Montrer que \(I_{n+1}\) est équivalent à \(I_n\) en \(+\infty\)
Montrer que \(\forall n \in \mathbb N, (n+1)I_{n+1}I_{n} = \)Cte
En déduire un équivalent simple de \(I_n\), puis sa limite

0 - Préliminaires

\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(sint)^n dt\end{align*}\)

La fonction \(x \mapsto sin(x)\) est de classe \(C^1\) sur l'intervalle \([0;\pi/2]\)
- Elle est continue , et dérivable sur cet intervalle
- Sa dérivée est continue
\(\forall n \space \in \mathbb N\), La fonction \(x \mapsto (sin(x)^n\) est aussi de classe \(C^1\) sur l'intervalle \([0;\pi/2]\)
\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(sint)^n dt\end{align*}\) existe

1 - Calculer \(I_0\) et \(I_1\)

\[\begin{align*} & I_n=\int_0^{\pi/2}sin^nt .dt \end{align*}\]
\(\begin{align*} & I_0 =\int_0^{\pi/2}sin^0t. dt =\int_0^{\pi/2}1 \times dt =\big[t \big]_0^{\pi/2} = \pi/2 \\
& I_1 =\int_0^{\pi/2}sin^1t. dt =\int_0^{\pi/2}sint.dt= \big[-cost\big]_0^{\pi/2} =-0-(-1) =1 \end{align*}\)

\[\boxed{I_0=\pi/2 \text{ et } I_1=1}\]

2 - Montrer que \((I_n)_{n \in \mathbb N}\) est bien définie

\[\begin{align*} & I_n=\int_0^{\pi/2}sin^nt .dt \end{align*}\]

Il faut démontrer que chaque terme de la suite (\(I_0\), \(I_1\), \(I_2\), \(I_3\), \(\dots\), \(I_n\) \(\dots\)) existent.
\(I_n\) est une intégrale: il faut donc que la fonction qui va être intégrée soit continue, faute de quoi l intégrale ne pourrait pas exister.

La fonction \(t \mapsto sin(t)\) est bien définie, continue et dérivable sur \(\mathbb R\), donc aussi sur l'intervalle sur \([0;\pi/2]\), et par conséquent la fonction \(t \mapsto sin^nt\) est bien définie, continue et dérivable sur \([0;\pi/2]\).

L'intégrale de la fonction \(t \mapsto sin^nt\) est calculable quelque soit la valeur de n.

Donc \(I_n\) est bien définie \(\forall n \in \mathbb N\)

3 - Montrer que \(\forall n \in \mathbb N, I_n = \int_0^{\pi/2}(cost)^n dt \) et en déduire \(I_2\)

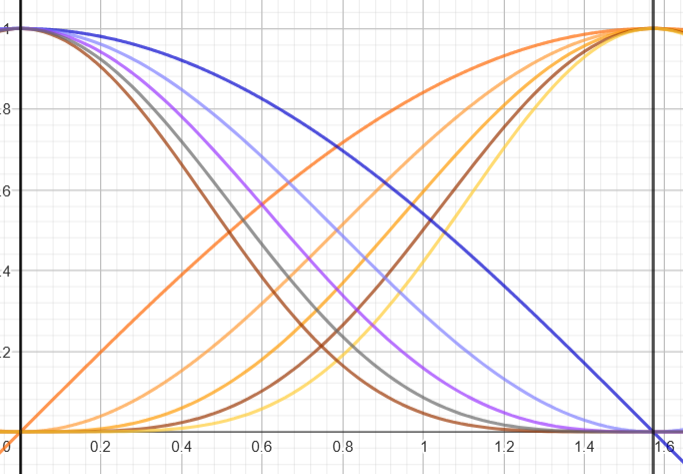
On peut essayer de tracer les fonctions \(sin^nt\) et \(cos^nt\) pour différentes valeurs de \(n\)

On observe immédiatement une symétrie / égalité de l'aire située sous les courbes \(sin^nt\) et \(cos^nt\). De façon générale, lorsqu'il s'agit de montrer ce genre d'égalité, de passer de \(cos\) à \(sin\), il faut pratiquer par changement de variable \(t=\pi/2-x\):

\(\begin{align*} \begin{cases} t=\pi/2-x \\ dt = -dx\end{cases} \Rightarrow \begin{cases} t=0 \Rightarrow x=\pi/2 \\ t = \pi/2 \Rightarrow x= 0 \end{cases} \end{align*}\)

\(\begin{align*} \forall n \in \mathbb N , I_n & = \int_{t=0}^{t=\pi/2} sin^nt.dt \\
& =\int_{x=\pi/2}^{x=0} sin^n(\pi/2-x) \times (-dx) \\
& = - \int_{\pi/2}^0 cos^nx . dx \\
& = \int_0^{\pi/2} cos^nx . dx \end{align*}\)

\[\boxed{ \begin{align*} \forall n \in \mathbb N, I_n & =\int_0^{\pi/2}sin^nt .dt= \int_0^{\pi/2}cos^nt .dt \end{align*}}\]

En calculant \(I_2\) de 2 façons , nous pouvons écrire que :
\( \begin{align*} I_2+I_2 & =\int_0^{\pi/2}sin^2t .dt+\int_0^{\pi/2}cos^2t .dt \\
& = \int_0^{\pi/2} [sin^2t +cos^2t ].dt \\
2 \times I_2 & = \int_0^{\pi/2} 1 \times dt = [t]_0^{\pi/2} = \pi/2\end{align*}\)

\[\boxed{I_2 = \pi/4}\]

4 - Montrer que \(I_n\) est convergente

Pour démontrer la convergence de \(I_n\), il faut:

montrer la monotonie de \(I_n\)
- trouver le signe de \(I_{n+1}-I_n \)
- une méthode plus analytique
minoration \ majoration de \(I_n\)
Convergence de \(I_n\)

calculer \(I_{n+1}-I_n\) :

\(\begin{align*}I_{n+1}-I_n & =\int_0^{\pi/2}sin^{n+1}t . dt-\int_0^{\pi/2}sin^nt .dt \\
& =\int_0^{\pi/2}[sin^{n+1}t -sin^nt] dt \\
& =\int_0^{\pi/2}sin^{n}t \times (sint-1) dt \\ \end{align*}\)

Sur \([0;\pi/2]\), on a: \(0 \leq sin(t) \leq 1\) \( \Rightarrow \begin{cases} sin^nt \geq0 \\ sin(t)-1 \leq 0 \end{cases} \)
donc \(sin^nt(sint-1) \leq 0\) et l'intégrale d'une fonction négative sur \([0;\pi/2]\) donne un résultat négatif.

Donc \(I_{n+1}-I_n \leq 0\) et \(I_n\) est décroissante.

Méthode plus analytique:

Sur \([0;\pi/2]\), on a :
\(\begin{align*} 0 & \leq sin(t) \leq 1 \\
\Rightarrow 0 & \leq sin^{n+1}t \leq sin^nt \end{align*}\).

Et par positivité de l'intégrale sur \([0;\pi/2]\),
\(\begin{align*} \int_0^{\pi/2}sin^{n+1}t.dt \leq \int_0^{\pi/2}sin^nt.dt \Rightarrow I_{n+1} \leq I_n \end{align*}\)

Donc \(I_n\) est décroissante.

Minoration / majoration de \(I_n\)

\(I_n\) étant décroissante , on va chercher une minoration afin de pouvoir affirmer la convergence:

Sur \(\begin{align*}[0;\pi/2] \space \space,\space \space sin(t) \geq 0 \Rightarrow sin^nt \geq 0 \end{align*}\)

Par conséquent \(I_n \geq 0\).

\(I_n \geq 0\)

Convergence de \(I_n\)

Nous avons démontrer que :

\(I_n\) est une suite décroissante
\(I_n \geq 0\), elle est donc minorée

D'aprés le Théorème des Suites Monotones Bornées, \(I_n\) est convergente

\(I_n\) est convergente

5 - Exprimer \(I_{n+2}\) en fonction de \(I_n\)

\(\begin{align*}\forall n \in \mathbb N, I_{n+2} &=\int_0^{\pi/2}sint^{n+2}t .dt \end{align*}\)

On sent bien ici qu'il nous faut couper \(sint^{n+2}t\) en 2 morceaux pour faire une intégration par parties. Mais comment le découper:

\(sin²t \times sin^{n}t\): cela semble assez difficile à intégrer par parties. De plus on a utilisé une astuce en 2 pour trouver \(I_2\)
\(1 \times sin^{n+2}t\) : dans ce cas, on se retrouve en faisant l'IPP avec du \( x \times sin^n \dots \) qui va être compliqué à trouver
\(sin(t) \times sint^{n+1}t\): en faisant l'IPP, on integre facilement le \(sin\) et on dérive facilement le \(sin^{n+1}\). On aura dans la 2ème partie du \(cos\) et du \(sin^n\) qui sera assez facilement intégrable

\(\begin{align*}I_{n+2} & = \int_0^{\pi/2}sint \times sin^{n+1}t . dt \end{align*}\)

Faisons une intégration par partie: \(\int u'v = [uv]- \int uv'\)
\(\begin{align*} \begin{cases} u'=sint \\ v = sin^{n+1}t\end{cases} \Rightarrow \begin{cases} u=-cost \\ v' = (n+1)sin^{n}t \times cost \end{cases} \end{align*}\)

Il ne faut pas oublier la "chain rule" quand on calcule \(v'\), c'est à dire le \(cos(t)\).

\(\begin{align*}\forall n \in \mathbb N, \\
I_{n+2} & = \int_0^{\pi/2}sint \times sin^{n+1}t . dt\\
&= \overbrace{[(- cost) \times sin^{n+1}t ]_0^{\pi/2}}^{=0} - \int_0^{\pi/2} (-cost)(n+1)sin^nt. cost .dt \\
& = \int_0^{\pi/2} cos^2t(n+1)sin^nt .dt \\
& = \int_0^{\pi/2} (1-sin^2t)(n+1)sin^nt .dt \\
& = \int_0^{\pi/2} [ (n+1)sin^nt-(n+1)sin^2t.sin^nt ]dt \\
& = (n+1)\int_0^{\pi/2} sin^nt.dt-(n+1)\int_0^{\pi/2}sin^{n+2}t .dt \\
I_{n+2}& =(n+1)I_n - (n+1)I_{n+2} \\
(n+2)I_{n+2} & = (n+1)I_{n} \end{align*}\)

avec \(n+2 \neq 0\) car \(n \in \mathbb N\)

Et pour finir, \[\boxed {\begin{align*}\forall n \in \mathbb N, I_{n+2} & = \frac{n+1}{n+2}I_n \end{align*}}\]

6 - Exprimer \(I_{2p}\) et \(I_{2p+1 }\) en fonction de \(p\), \(\forall p \in \mathbb N\)

Calcul de \(I_{2p}\)

On cherche à exprimer \(I_{2p}\). Or d'après 5, \(I_{2p}\) s'exprime en fonction de \(I_{2p-2}\). La relation trouvée en 5 ne peut pas être valable pour \(p=0\) car \(I_{-2}\) n'existe pas. En effet \(I_n\) est définie \(\forall n \in \mathbb N\)

Commençons alors par chercher \(I_{2p}\) en fonction de \(p\) pour \(p \in \mathbb N^*\). Nous vérifierons le résultat avec \(p=0\) ensuite.

\(\begin{align*} \forall n \in \mathbb N, I_{n+2} = \frac{n+1}{n+2} I_n \end{align*} \Leftrightarrow I_{nombre}= \frac{nombre-1}{nombre} \times I_{nombre-2}\)

\(\begin{align*} \Rightarrow I_{2p} & = \frac{2p-1}{2p}I_{2p-2}, \space \forall p \in \mathbb N^*\\
& = \frac{2p-1}{2p} \times \frac{2p-3}{2p-2} \times I_{2p-4} \\
& = \frac{2p-1}{2p} \times \frac{2p-3}{2p-2} \times \frac{2p-5}{2p-4} \times I_{2p-6} \\
& = \frac{2p-1}{2p} \times \frac{2p-3}{2p-2} \times \frac{2p-5}{2p-4}\dots \times \frac{3}{4} \times \frac{ 1}{2} \times I_{0} \\
& = \frac{impairs}{paires} \times I_0 \end{align*}\)

Dans ce genre de cas , l'astuce consiste à multiplier le haut et le bas par les nombres paires, ainsi au numérateur, on se retrouvera avec du \(2p!\), et au dénominateur, a condition de factoriser par 2 chaque terme (ils sont pairs) on retrouvera aussi du \(p!\).

\(\begin{align*}\Rightarrow I_{2p} & = \frac{2p-1}{2p} \times \frac{2p-3}{2p-2} \times \frac{2p-5}{2p-4} \times \dots \times \frac{3}{4} \times \frac{ 1}{2} \times I_{0} \\
& = \frac{2p(2p-1)(2p-2)(2p-3)(2p-4)(2p-5)\dots(2)(1)}{\bigg[\underbrace{2p(2p-2)(2p-4)(2p-6)\dots 2(1)}_{\text{il y a p fois le terme 2}}\bigg]^2}I_0 \\
& = \frac{(2p)!}{\bigg[2^p \times \big[p(p-1)(p-2)\dots(2)(1)\big] \bigg]^2}I_0 \\
& = \frac{(2p)!}{\bigg[2^p \times p! \bigg]^2}I_0 \\
& = \frac{(2p)!}{2^{2p}(p!)^2}I_0 \end{align*}\)

Avec \(I_0=\pi/2\) comme vu à la question 1

\[\boxed {\begin{align*}I_{2p} & = \frac{(2p)!}{2^{2p}(p!)²}\frac{\pi}{2}, \space \forall p \in \mathbb N^* \end{align*} }\]

Il nous reste à régler le problème pour \(p=0\)

Si \(p=0\) alors: \(\begin{align*} \begin{cases}\text{d'après la question 1 : }I_0 =\pi/2 \\
\text{d'après la question 6 : }\begin{cases} I_{2p} & = \frac{(2p)!}{2^{2p}(p!)²}\frac{\pi}{2} \\
I_0 & = \frac{(0)!}{2^{0}(0!)²} \times \frac{\pi}{2} \\
& =\frac{1}{1}\pi/2 \\
& = \pi/2 \end{cases} \end{cases} \end{align*}\)

La relation trouvée ci-dessus est valable aussi pour \(p=0\)

\[ \boxed{ \begin{align*}\forall p \in \mathbb N , \space I_{2p}= \frac{(2p)!}{2^{2p}(p!)²}\frac{\pi}{2} \end{align*}} \]

Calcul de \(I_{2p+1}\)

On répète le même procédé pour calculer \(I_{2p+1}\) en fonction de \(p\)
On cherche à exprimer \(I_{2p+1}\). Or d'après 5, \(I_{2p+1}\) s'exprime en fonction de \(I_{2p-1}\). La relation trouvée en 5 ne peut pas être valable pour \(p=0\) car \(I_{-1}\) n'existe pas. En effet \(I_n\) est définie \(\forall n \in \mathbb N\)

Commençons alors par chercher \(I_{2p+1}\) en fonction de \(p\) pour \(p \in \mathbb N^*\). Nous vérifierons le résultat avec \(p=0\) ensuite.

\(\begin{align*} \forall n \in \mathbb N, I_{n+2} = \frac{n+1}{n+2} I_n \end{align*} \Leftrightarrow I_{nombre}= \frac{nombre-1}{nombre} \times I_{nombre-2}\)

\(\begin{align*}I_{2p+1} & = \frac{2p}{2p+1}I_{2p-1}, \space \forall p \in \mathbb N^* \\
& = \frac{\overbrace{2p(2p-2)(2p-4)(2p-6)\dot(4)(2)}^{\text{p fois le facteur 2}}}{(2p+1)(2p-1)(2p-3)\cdot (3)(1)}I_1 \\
& = \frac{\bigg[2p \times (2p-2)(2p-4)(2p-6)\dot(4)(2)\bigg]^2}{(2p+1)(2p)(2p-1)\cdot (2)(1)}I_1 \\
& = \frac{\bigg[2^p \times p(p-1)(p-2)(p-3\dot(2)(1)\bigg]^2}{(2p+1)!}I_1 \\
& = \frac{[2^p \times p!]^2}{(2p+1)!}I_1 \\
& = \frac{2^{2p}(p!)²}{(2p+1)!}I_1\end{align*}\)

avec \(I_1=1\)

\[\begin{align*}\boxed{ I_{2p+1}= \frac{2^{2p}(p!)²}{(2p+1)!}, \space \forall p \in \mathbb N^* } \end{align*}\]

Il nous reste à régler le problème pour \(p=0\)

Si \(p=0\) alors: \(\begin{align*} \begin{cases}\text{d'après la question 1 : }I_1 =1 \\
\text{d'après la question 6 : }\begin{cases} I_{2p+1} & = \frac{2^{2p}(p!)²}{(2p+1)!} \\
I_1 & = \frac{(2^0) \times 0!}{(2 \times0 + 1)!} \\
& =\frac{1 \times 1}{1!} \\
& = 1 \end{cases} \end{cases} \end{align*}\)

La relation trouvée ci-dessus est valable aussi pour \(p=0\)

\[\begin{align*}\boxed{ I_{2p+1}= \frac{2^{2p}(p!)²}{(2p+1)!}, \space \forall p \in \mathbb N } \end{align*}\]

7 - Montrer que \(I_{n+1}\) est équivalent à \(I_n\) en \(+\infty\)

Pour montrer que \( I_{n+1}\) \( \widetilde{+ \infty}\) \( I_{n} \), montrons que \(\frac{I_{n+1}}{I_n} \space \widetilde{+\infty} \space1 \)

Il faut commencer alors par montrer que \(\forall n \in \mathbb N, I_n \neq 0\) pour pouvoir diviser par \(I_n\)

Sur \(]0;\pi/2]\),

\( sin(t) > 0\)
\(sin^nt > 0\)

Comme \(sin(t)\) n 'est pas la fonction constante égale à \(0\), alors son intégrale est strictement supérieure a \(0\) et

\[\forall n \in \mathbb N, I_n \neq 0 \]

\(I_n \) est décroissante (d'aprés la question 4) donc: \(\forall n \in \mathbb N\)

\(\begin{align*}
I_{n+2} & \leq I_{n+1} \leq I_{n} \\
\frac{I_{n+2}}{I_{n}} & \leq \frac{I_{n+1}}{I_{n}} \leq 1 \\
\frac{n+1}{n+2} & \leq \frac{I_{n+1}}{I_{n}} \leq 1\\
1 & \leq \frac{I_{n+1}}{I_{n}} \leq 1 \end{align*}\)

car \(\begin{align*} & \lim \limits_{n \to + \infty}\frac{n+1}{n+2}= \lim \limits_{n \to + \infty}\frac{1+\cancel{\frac{1}{n}}}{1+\cancel{\frac{2}{n}}} = 1\end{align*}\)

D'après le Théorème des gengarmes: \(\lim \limits_{n \to + \infty}\frac{I_{n+1}}{I_{n}}=1\) et \(\frac{I_{n+1}}{I_{n}} \widetilde{+\infty }1\) et en définitive:

\[ \boxed{\forall n \in \mathbb N, I_{n+1}\widetilde{+\infty }I_{n}}\]

8 - Montrer que \(\forall n \in \mathbb N, (n+1)I_{n+1}I_{n} = \) Cte

La difficulté réside dans le fait que nous avons une suite constante, mais qui n 'a pas de nom. Donc nommons la en posant: \(\forall n \in \mathbb N, U_n= (n+1)I_{n+1}I_{n}\) et Calculons \(U_{n+1}\):

\(\begin{align*}& \forall n \in \mathbb N, \\
U_{n+1} & = [(n+1)+1] \times I_{(n+1)+1} \times I_{(n)+1} \\
& = (n+2) \times I_{n+2} \times I_{n+1} \\
& = \cancel{(n+2)} \times \frac{n+1}{\cancel{n+2}}I_n \times I_{n+1} \\
& = (n+1) \times I_{n+1} \times I_n \\
& = U_n\end{align*}\)

Si \(\forall n \in \mathbb N, U_{n+1} = U_n\), alors \(U_n\) est constante.

Quand on demande de démontrer que quelque chose est constant, il est toujours demandé implicitement de trouver cette constante.
\(U_n=U_0 =(0+1) \times I_1 \times I_0 =1 \times 1 \times \pi/2\)

\[\boxed{ \forall n \in \mathbb N, (n+1)I_{n+1}I_{n}=\pi/2}\]

9 - En déduire un équivalent simple de \(I_n\), puis sa limite

D'après la question 8 , \(\forall n \in \mathbb N, (n+1)I_{n+1}I_{n}= \pi/2\)
D'après la question 7 , \(I_{n+1} \widetilde{+ \infty} I_{n}\)
D'après la question 4, \(I_n>0\)
\(n \to + \infty\)

En conséquence:

\((n+1)I_{n+1}I_{n} \space\widetilde{+ \infty} \space (n\times I_n \times I_n ) \\
\Rightarrow \pi/2 \space \widetilde{+ \infty} \space n I_n^2 \\
\Rightarrow I_n^2 \space \widetilde{+ \infty} \space \frac{\pi}{2n} \\
\Rightarrow \lvert I_n \rvert \space \widetilde{+ \infty} \space \sqrt{\frac{\pi}{2n}} \\
\Rightarrow I_n \space \widetilde{+ \infty} \space \sqrt{\frac{\pi}{2n}} \) car \(I_n \gt 0\)

\[\boxed{ I_n \space \widetilde{+ \infty} \space \sqrt{\frac{\pi}{2n}} }\]

\(\lim \limits_{n \to + \infty}I_n = \lim \limits_{n \to + \infty} \sqrt{\frac{\pi}{2n}}=0\)
par composition des limites.

\[\boxed {\lim \limits_{n \to + \infty}I_n=0} \]

Les intégrales de Wallis - 1