En mathématiques, les polynômes de Laguerre, nommés d'après Edmond Laguerre, sont les solutions normalisées de l'équation de Laguerre : \[ xy"+(1-x)y'+ny=0\] qui est une équation différentielle linéaire homogène d'ordre 2 et se réécrit sous la forme de  Sturm-Liouville: \(−\frac{d}{dx} \Bigg(xe^−x \frac{dy}{dx} \Bigg)=n e^{−x} y\) Les polynômes de Laguerre apparaissent en mécanique quantique dans la partie radiale de la solution de l'équation de Schrödinger pour un atome à un électron. Le coefficient dominant de \(L_n\) est \(\frac{(–1)^n}{n!}\). Les physiciens utilisent souvent une définition des polynômes de Laguerre où ceux-ci sont multipliés par \(\frac{(–1)^n}{n!}\), obtenant ainsi des polynômes unitaires.

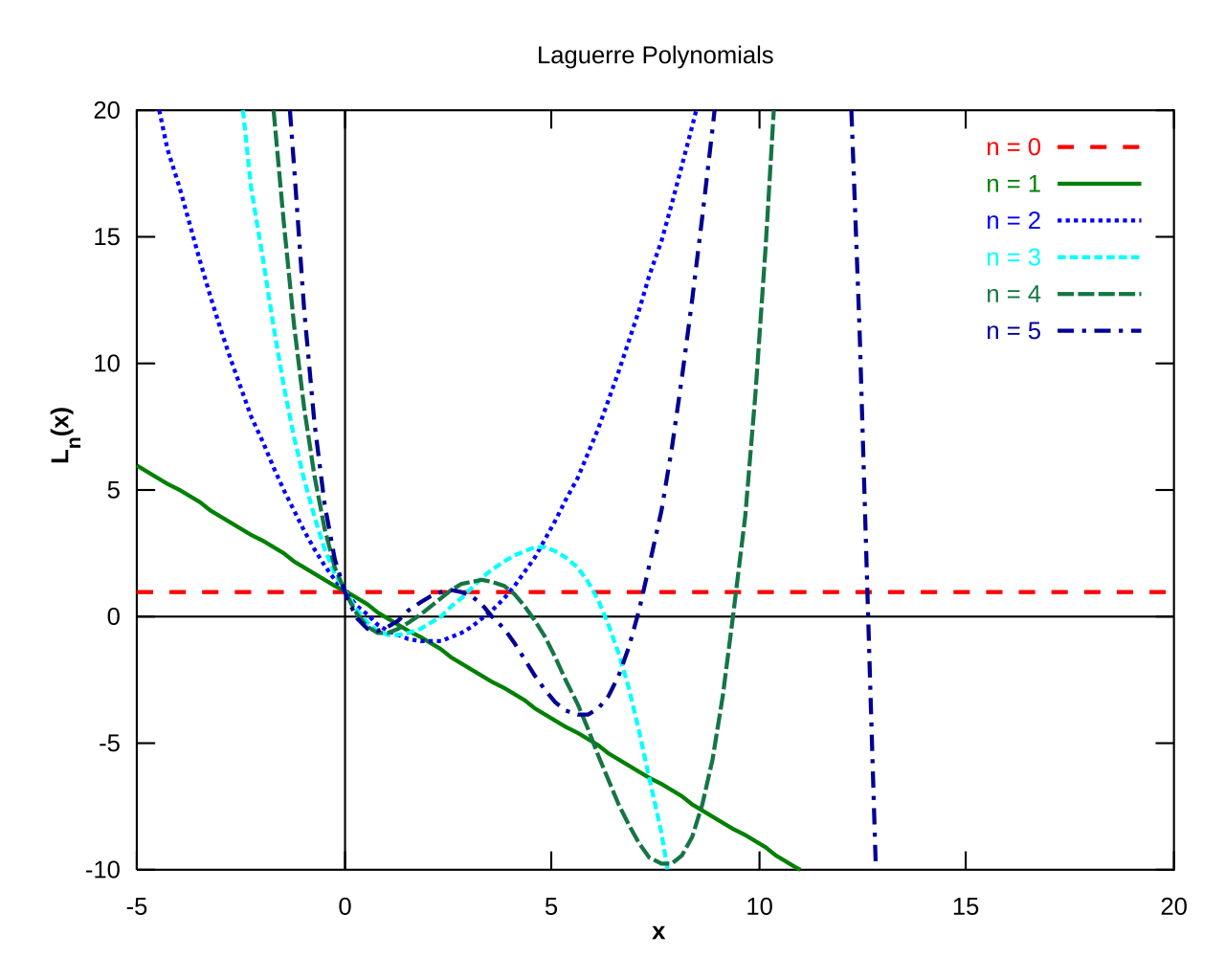
Les polynômes de Laguerre sont des polynômes définis par : \(\begin{align*} L_n(x) = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) }\end{align*}\) ou (\(x^n e^{-x} )^{ (n) }\) est la dérivée nième de \(x^n e^{-x} \).

1. Calculer \(L_0\), \(L_1\), \(L_2\)
2. Montrer en utilisant la formule de Leiniz généralisée que \(\begin{align*} L_n(x) = \sum\limits_{k=0^n} \binom{n}{k}\frac{(-x)^k}{k!}    \end{align*}\). Vérifier pour \(L_2\)
3. Remarquer que \(\forall n \in \mathbb N, \space L_n(0)=1\).
4. Montrer que  \(\begin{align*} \forall n \in \mathbb N, \space I_n=\int_0^{+\infty} \frac{1}{n!}x^ne^{-x}dx   =1  \end{align*}\)
5. Montrer que pour \(n \in \mathbb N; \space 0 \leq k \leq n, \space \big(e^{-x}x^n \big)^{(k)} = \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}\)
6. En déduire que \(\forall n \in \mathbb N^*, \space 0 \leq k \lt n\) et \(Q \in \mathbb R[X]\), on a : \(\big[ (e^{-x}x^n)^{(k)}Q(x)\big]_0^{+\infty}=0\)
7. Soit \(E= \mathbb R[X]\) muni de la fonction \(\begin{align*} (P,Q) \in E^2 \mapsto \langle P,Q \rangle = \int_0^{+\infty}P(x)Q(x)e^{-x}dx \end{align*}\). Montrer que \(\langle P;Q \rangle\) définit un produit scalaire.

\[\begin{align*} L_n(x) = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) }\end{align*}\]

\(\begin{align*} L_0(x) = \frac{e^x}{0!}(x^0 e^{-x} )^{ (0) } = e^x(1 \times e^{-x} )^{ (0) }=e^x \times e^{-x}=e^0 = 1\end{align*}\)

\(\begin{align*} L_1(x) & = \frac{e^x}{1!}(x^1 e^{-x} )^{ (1) } = e^x(xe^{-x})' = e^x[e^{-x}-xe^{-x} ] \\
& = e^x \times [e^{-x}(1-x) ]  = 1-x\end{align*}\)

\(\begin{align*} L_2(x) & = \frac{e^x}{2!}(x^2 e^{-x} )^{ (2) } = \frac{e^x}{2}(x^2 e^{-x} )" = \frac{e^x}{2} \times [2x e^{-x}-x^2e^{-x}]'  \\
& = \frac{e^x}{2} [2 e^{-x} - 2x e^{-x} - 2x e^{-x} + x^2 e^{-x} ] = \frac{e^x}{2} \times e^{-x}[2-2x-2x - x^2 ] \\& =\frac{1}{2}(2-4x+x^2) \end{align*}\)

Formule de Leibniz généralisée :

Posons : \(f(x) = e^{-x} \) et \(g(x) =x^{n}\), alors \(f\) et \(g\) sont de classe \(C^\infty\). Calculons \(f^{(k)}\) et \(g^{(n-k)}\)

• \(f(x) = e^{-x} \Rightarrow f^{(k)} = (-1)^k e^{-x}\)
  
  
• \(g(x) =x^{n}\)
  \( g'(x)= nx^{n-1}\), \( g''(x)= n(n-1)x^{n-2}\) \(\Rightarrow g^{(n)}(x) = n!x^0=n!\)
  On cherche une expression de \(g^{(n-k)}\)
  dérivée d'ordre n (\(k=0\)):  \( = n!= n!x^{0}= \frac{n!}{0!}x^{k} = \frac{n!}{k!}x^{k}\)
  dérivée d 'ordre 0 (\(k=n\)): \( = x^{n} =\frac{n!}{n!} x^{n} =\frac{n!}{k!} x^{k}\)
  dérivée d 'ordre 1 (\(k=n-1\)): \( = n x^{n} =\frac{n!}{(n-1)!} x^{n-1}= \frac{n!}{k!} x^{k} \)
  dérivée d 'ordre 2 (\(k=n-2\)): \( = n(n-1)x^{n-2} = \frac{n!}{1 \times 2 \times \cdots \times(n-2)}x^{n-2} = \frac{n!}{k!}x^{k} \)
  dérivée d 'ordre 3 (\(k=n-3\)): \( = n(n-1)(n-2)x^{n-3}= \frac{n!}{1 \times 2 \times \cdots \times(n-3)}x^{n-3} = \frac{n!}{k!}x^{k} \)
  \(\Rightarrow g^{(n-k)} = \frac{n!}{k!} x^{k}\)
  
  
• Calculons \(L_2(x)\)
  \(\begin{align*} L_n(x) & = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) } \\ 
  & = \frac{e^x}{n!}  \sum\limits_{k=0}^n \binom{n}{k} f^{(k)} g^{(n-k)}  \\ 
  & = \frac{\cancel{e^x}}{\cancel{n!}} \sum\limits_{k=0}^n \binom{n}{k}(-1)^k \cancel{e^{-x}} \frac{\cancel{n!}}{k!}x^{k} = \sum\limits_{k=0}^n \binom{n}{k}(-1)^k  \frac{x^{k}}{k!}= \sum\limits_{k=0}^n \binom{n}{k}  \frac{(-x)^{k}}{k!} \end{align*}\)

\(\begin{align*} L_2(x) & = \sum\limits_{k=0}^2 \binom{2}{k}  \frac{-x^{k}}{k!} \\
& = \underbrace{\binom{2}{0}}_{1}  \frac{(-x)^{0}}{0!} + \binom{2}{1}  \frac{(-x)^{1}}{1!} + \binom{2}{2}  \frac{(-x)^{2}}{2!} \\
& = 1 - 2x +\frac{x^2}{2} = \frac{1}{2}(2-4x+x^2) \end{align*}\)

\(\begin{align*} L_n(x) = \sum\limits_{k=0}^n \binom{n}{k}  \frac{(-x)^{k}}{k!} \end{align*}\)

\(\begin{align*} L_n(0) & = \sum\limits_{k=0}^n \binom{n}{k}  \frac{(0)^{k}}{k!} \\
& = \binom{n}{0}  \frac{(0)^{}}{0!} +\cancel{ \binom{n}{1}  \frac{(0)^{1}}{1!}}+ \cancel{\binom{n}{2}  \frac{(0)^{2}}{2!}} + \dots \dots\\
& = 1 \times \underbrace{\frac{(0)^{0}}{0!}}_{1} + 0+0+ \cdots =1  \end{align*}\)

En effet :\(L_0(0) = L_1(0) =L_2(0)=1\)

\(\begin{align*}   I_0 & =\int_0^{+\infty} \frac{1}{0!}x^0e^{-x}dx   \\
& = \int_0^{+\infty} e^{-x}dx = \bigg[ -e^{-x}\bigg]_0^{+\infty}
= 0 - (-1) = 1\end{align*}\)

Par récurrence: Soit la proposition \(P_n\):  \(I_n=\int_0^{+\infty} \frac{1}{n!}x^ne^{-x}dx   =1\)

• Initialisation:
  par calcul ci-dessus: \(I_0 = 1\)
  par hypothèse: \(_0=1\)
  La proposition \(P_n\) est vraie pour \(n=0\)
  
  
• Récurrence:
  Supposons la proposition \(P_n\) vraie au rang \(n\), soit : \(I_n=1\)
  Montrons qu'elle est vraie au rang \(n+1\), soit : \(I_{n+1}=1\)
  Calculons \(I_{n+1}\) par IPP:
  \(\begin{align}I_{n+1} & =\int_0^{+\infty} \frac{1}{(n+1)!}\underbrace{x^{n+1}}_{u} \underbrace{e^{-x}}_{v'}dx \\
  & = \cancel{ \bigg[ x^{n+1}(-e^{-x}) \bigg]_0^{+\infty}} + \int_0^{+\infty} \frac{1}{(n+1)!}(n+1)x^{n} e^{-x}dx  \\
  & = \int_0^{+\infty} \frac{1}{n!}x^{n} e^{-x}dx  = I_n = 1\end{align} \) 
  
  
• Conclusion: 
  La proposition \(P_n\) : \(I_n=\int_0^{+\infty} \frac{1}{n!}x^ne^{-x}dx   =1\) est vraie au rang \(n=0\), si elle est vraie au rang \(n\), alors elle est vraie au rang \(n+1\). Elles est donc vraie \(\forall n \in \mathbb N\)
  
  

On veut montrer que la dérivée de \(e^{-x}x^n\) , est de la forme \(e^{-x}Q(x)\), où \(Q(x)\) est un polynôme.

Démontrons par récurrence sur \(k\):
Soit la proposition \(P_k\): \((e^{-x}x^n \big)^{(k)} = \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}\) 

• Initialisation:
  

  Pour \(k= 0\) :
  Par calcul: \((e^{-x}x^n \big)^{(0)} = e^{-x}x^n = e^{-x}x^n\)
  Par hypothèse : \((e^{-x}x^n \big)^{(0)} = \big( \sum\limits_{j=n-0}^{n}a_jx^j \big)e^{-x} = a_nx^ne^{-x}=e^{-x}x^n\) avec \(a_n=1\)
  La proposition \(P_k\) est vraie pour \(k= 0\)

• Récurrence:
  Supposons la proposition \(P_k\) vraie au rang \(k\): \((e^{-x}x^n \big)^{(k)} = \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}\)
  Montrons qu'elle est vraie au rang \(k+1\): \((e^{-x}x^n \big)^{(k+1)} = \big( \sum\limits_{j=n-k-1}^{n}a_jx^j \big)e^{-x}\)
  \(\begin{align*} (e^{-x}x^n \big)^{(k+1)} & =  \bigg[ \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}  \bigg]' \\
  & = - \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x} + \big( \sum\limits_{j=n-k}^{n}j.a_jx^{j-1} \big)e^{-x} \\
  & = e^{-x} \bigg[ -  \sum\limits_{j=n-k}^{n}a_jx^j +  \sum\limits_{j=n-k}^{n}j.a_jx^{j-1} \bigg] \\
  & = e^{-x} \bigg[\underbrace{ -  \sum\limits_{j=n-k}^{n}a_jx^j +  \sum\limits_{j=n-(k+1)}^{n}(j+1).a_{j+1}x^{j}}_{\text{polynôme de degré n}} \bigg]  = \big( \sum\limits_{l=n-k}^{n}a_lx^l \big)e^{-x} \end{align*}\)
  La propriété \(P_k\) est vraie au rang \(k+1\)
  
  
• Conclusion:
  La proposition \(P_k\) est vraie au rang \(k=0\), si elle est vraie au rang \(k=n\), alors elle est vraie au rang \(k+1\). Donc elle est vraie \(\forall n \in \mathbb N\).

Soit \(u(x) = (e^{-x}x^n)^{(k)}Q(x)\), 
Pour \(k \lt n\) (donc \(\underline{n \gt 0}\)) , le degré de \(\big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x} \gt 0\), donc il possède au moins un terme en \(x\), et on peut factoriser par \(x\). Alors on peut écrire : 
\(\begin{align} u(x) & = (e^{-x}x^n)^{(k)}Q(x) =\big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}Q(x) \\
& = x\big( \sum\limits_{l=n-k}^{n}a_lx^{l-1} \big)e^{-x} Q(x) = x e^{-x} \underbrace{\big( \sum\limits_{l=n-k}^{n}a_lx^{l-1} \big)Q(x)}_{P(x) \in \mathbb R[X]} \\
& =  x e^{-x}P(x) \end{align}\)

\(\begin{align}  \begin{cases}  x e^{-x}P(x) \xrightarrow{x = 0} 0 \\ x e^{-x}P(x) \xrightarrow{x \to +\infty} 0 \text{ par croissance comparée} \end{cases}  \Longrightarrow \big[ (e^{-x}x^n)^{(k)}Q(x)\big]_0^{+\infty}=0\end{align}\)

1 - Existence de l'intégrale qui définit \(\langle P,Q \rangle\)

2 - Rappels de cours

3 - Forme symétrique :\(\langle P|Q \rangle = \langle Q|P \rangle\)  ??

4 - Forme bilinéaire ??

5 - Forme définie positive ??