\(\begin{align*}\int \sqrt{(x²+4x+13)}.dx \end{align*}\)

\(\begin{align*} I  & = \int \sqrt{(x²+4x+13)}.dx \end{align*}\)

Nous avons ici un polynome du 2nd degré non factorisable sous un radical. Notre chance de nous en sortir est d'aller chercher une forme en \( tan²x + 1 = sec²x \), ce qui nous permettra de retirer le radical.
A réaliser :

• factoriser et se ramener a une forme \(u²+1\)
• faire un changement de variable
  • \(tan\theta=u\) et revenir a une forme en \(x\)

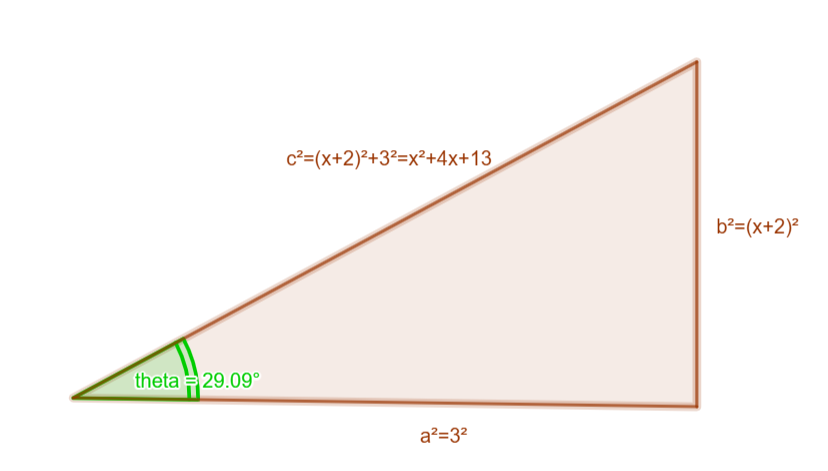
Ici nous avons presua un carré parfait avec \(x²+4x+........\). Alors écrivons que \(x²+4x=(x+2)²-4\) 

\(\begin{align*}
I & =\int \sqrt{[(x+2)²-4+13]}.dx  = \int \sqrt{[(x+2)²+9]}.dx\\
& = \int \sqrt{[(x+2)²+3²]}.dx = \int \sqrt{9[(\frac{(x+2)²}{9}+\frac{9}{9}]}dx \\
& =  \int 3 \sqrt{(\frac{x+2}{3})²+1}dx = 3 \int  \sqrt{(\frac{x+2}{3})²+1}dx
\end{align*}\)

Procédons maintenant à un changement de variable de façon a retrouver une forme en \(tan²x +1\) et retrouver ensuite \(sec²x\):

\( \begin{align*} & \begin{cases} tan \theta=\frac {x+2}{3} \Rightarrow 3.tan \theta = x+2 \\ dx= 3sec² \theta .d \theta\end{cases} \\ \\
I & =3 \int \sqrt{tan² \theta+1} \times 3sec² \theta .d \theta \\
& = \int 9 \sqrt{sec² \theta} sec² \theta .d \theta \\
& = 9 \int sec^{3} \theta .d \theta \\
& = 9 \big[ \frac{1}{2} (sec \theta . tan \theta + ln \lvert sec \theta+  tan \theta \rvert) \big] +C \\
& = \frac{9}{2} \big[  (sec \theta . tan \theta + ln \lvert sec \theta+  tan \theta \rvert) \big] +C
\end{align*}\)

Cette dernière ligne trouve sa justification dans l'exercice 24.

Revenons maintenant à la variable \(x\), et commençons par un petit schéma: nous avons \(tan \theta = \frac{x+2}{3}\) qui nous permet de dessiner un triangle rectangle dont nous connaissons les 3 côtés.

Dans ce triangle rectangle, il sera possible de retrouver les differentes fonctions trigonométriques dont nous auront besoin pour trouver \(I\) et terminer l'exercice.

\( \begin{align*}
I & = \frac{9}{2} \big[  (sec \theta . tan \theta + ln \lvert sec \theta+  tan \theta \rvert) \big] +C \\
& \text{Avec: } \begin{cases} sec\theta = \frac{1}{cos\theta} = \frac{\sqrt{x²+4x+13}}{3} \\ tan\theta = \frac{x+2}{3}\end{cases} \\ \\
I & = \frac{\cancel{9}}{2} \frac{\sqrt{x²+4x+13}}{\cancel{3}}.\frac{x+2}{\cancel{3}} + \frac{9}{2} ln \bigg\lvert \frac{\sqrt{x²+4x+13}}{3}+\frac{x+2}{3} \bigg\rvert + C_1 \end{align*}\)
D'après le schéma ci dessus et parce qu'on est dans un triangle rectangle, on a:  
\( \begin{align*} \forall x: \sqrt{x²+4x+13} \geq x+2 \end{align*}\)
On peut donc retirer les valeurs absolues.
\( \begin{align*}I & = \frac{1}{2}(x+2)\sqrt{x²+4x+13}+\frac{9}{2}ln \frac{1}{3} \bigg[\sqrt{x²+4x+13}+(x+2) \bigg] + C_1\\
& = \frac{1}{2}(x+2)\sqrt{x²+4x+13}+\frac{9}{2} \bigg[\cancel {ln \frac{1}{3}}^{=cte} + ln \bigg[\sqrt{x²+4x+13}+(x+2)\bigg] \bigg] + C_1 \\
& = \frac{1}{2}(x+2)\sqrt{x²+4x+13} + \frac{9}{2}ln \bigg[\sqrt{x²+4x+13}+(x+2)\bigg]  + C_2
\end{align*}\)

\[\boxed{I = \frac{1}{2}(x+2)\sqrt{x²+4x+13} + \frac{9}{2}ln \bigg[ \sqrt{x²+4x+13}+(x+2) \bigg] + C_2 \in \mathbb R}\]

\(\begin{align*}\int csc x. dx\end{align*}\) a verifier 

\(\begin{align*}I = \int csc x. dx\end{align*}\)

Je vous recommande de vous reporter à l'exercice 25 ou au chapitre "A savoir" et au calcul de \(\int secx.dx\). La méthode est similaire.

\(\begin{align*}
I & = \int csc x. dx \\
& = \int \frac{cscx (cscx-cotx)}{cscx-cotx}dx \\
& or \begin{cases} u= cscx - cot x \\ du = -cscx .cot x
\end{cases} \\
I & = ln \lvert  csc x - cot x \rvert + C
\end{align*}\)

\[ \boxed {I  = ln \lvert  csc x - cot x \rvert + C (\in \mathbb R)}\]

\(\begin{align*}\int cos \sqrt{x}.dx\end{align*}\)

\(\begin{align*}I & = \int cos \sqrt{x}.dx \\
& \text{Changement de vatiable } \begin{cases} u=\sqrt{x}  \\ u²=x \\ 2u.du = dx \end{cases} \\
I & = \int cosu \times 2u.du \\
\end{align*}\)

Ces 2 fonctions se primitivent et se dérivent facilement , ce qui nous indique une IPP:

\(\begin{align*}
I & = \int cosu \times 2u.du \\
& = 2u.sin u +2cos u +C \\
& = 2 \sqrt{x}.sin \sqrt{x} +2cos \sqrt{x} +C
\end{align*}\)

\[\boxed{I = 2 \sqrt{x}.sin \sqrt{x} +2cos \sqrt{x} +C (\in \mathbb R)}\]

\(\begin{align*} \int \frac{1}{x \sqrt{9x²-1}}dx\end{align*}\)

\(\begin{align*}I & = \int \frac{1}{x \sqrt{9x²-1}}dx\end{align*}\)

Remarques:

1. Techniquement, il faut voir le \(9x²\) comme étant \((3x)²\) puis pratiquer un changement de variable.
2. Par expérience , si on rencontre la forme \(\frac{1}{x \sqrt{(ax)²-1}}\) alors la réponse est du style \( sec^{-1} \sqrt{ax} + C\)
3. on sait que \(sec²x-1=tan²x\) , ce qui implique le changement de variable \(3x=sec\theta\)

Procédons au changement de variable permettant de résoudre cette intégrale: 

\(\begin{align*}
I & = \int \frac{1}{x \sqrt{9x²-1}}dx \\
& =  \int \frac{1}{x \sqrt{(3x)²-1}}dx \\
& \text{Posons } \begin{cases}3x=sec \theta  \\ \theta = sec^{-1}(3x) \end{cases} \Rightarrow \begin{cases} x=\frac{1}{3}sec \theta \\ dx= \frac{1}{3}sec \theta.tan \theta .d \theta \end{cases}\\
I & = \int  \frac{1}{\cancel{\frac{1}{3}}\cancel{sec \theta} . \sqrt{sec² \theta-1}}\cancel{\frac{1}{3}}\cancel{sec \theta}.tan \theta .d \theta \\
& = \int \frac{tan \theta}{\sqrt{tan² \theta}}d \theta  \\
& = \int \frac{tan \theta}{tan \theta}d \theta  \\
& = \theta +C
\end{align*}\)

\[\boxed{I = sec^{-1}(3x) +C (\in \mathbb R)}\]