Description
Résoudre C=Acos(x) + Bsin(x)
Il existe plusieurs méthodes pour résoudre ce genre d'équation:
- partant de C, on calcule en connaissant l'objectif à atteindre: \(C= \rho.cos(\phi-x)\)
- on veut écrire \(C=A.cosx+B.sinx=Rcos(x+\phi)\): on développe...
- on veut écrire \(C=A.cosx+B.sinx=Rsin(x+\phi)\): on développe...
Méthode 1:
|
\begin{align*} \[\boxed{ A.cosx+B.sinx =\rho.cos(\phi-x) \text{ avec : } \\ \begin{cases} \rho=\sqrt{A²+B²} \text{ ou } \rho²=A²+B² \\ cos\phi=\frac{A}{\rho} \end{cases} } \] |
Méthode 2:
|
On veut comme résultat: \(C=A.cosx+B.sinx=R.sin(x+\phi)\) Et en utilisant les formules d'addition: \begin{align*} R.sin(x+\phi) & = R.cosx.sin\phi+R.sinx.cos\phi \\ & = (R.sin\phi).cosx+(Rcos\phi).sinx \\ & =A.cosx+B.sinx \end{align*} Par identification: \(\begin{cases} A=R.sin\phi \\ B=R.cos\phi \end{cases}\Rightarrow \begin{cases}tan\phi=A/B \\ A²+B²=R²(cos²\phi+sin²\phi)=R² \end{cases}\) \[\boxed{ Acosx + Bsinx = Rsin(x+\phi) \\ \text{avec }\begin{cases} \sqrt{A²+B²}=R \\ tan\phi = A/B \end{cases}}\]
Exemple: mettre \(cosx+sinx\) sous la forme \(R.sin(x+\phi)\) \(A=1 \text{ et } B=1 \Rightarrow \begin{cases} R=\sqrt{2} \\ tan\phi=1 \Rightarrow \phi = \pi/4 \end{cases}\) \(cosx+sinx=\sqrt{2}.sin(x+\pi/4)\) |
Méthode 3:.
|
On veut comme résultat: \(C=A.cosx+B.sinx=R.cos(x+\phi)\) Et en utilisant les formules d'addition: \(\begin{align*} R.cos(x+\phi) & = R.cosx.cos\phi+R.sinx.sin\phi \\ & = (R.cos\phi).cosx+(Rsin\phi).sinx \\ & =A.cosx+B.sinx \end{align*}\) Par identification: \(\begin{cases} A=R.cos\phi \\ B=R.sin\phi \end{cases}\Rightarrow \begin{cases}tan\phi=B/A \\ A²+B²=R²(cos²\phi+sin²\phi)=R² \end{cases}\) \[\boxed{ Acosx + Bsinx = Rcos(x+\phi) \\ \text{avec }\begin{cases} \sqrt{A²+B²}=R \\ tan\phi = B/A \end{cases}}\] On notera la symétrie de \(tan\phi\) par rapport a la méthode 2.
Exemple: mettre \(cosx+sinx\) sous la forme \(R.cos(x+\phi)\) \(A=1 \text{ et } B=1 \Rightarrow \begin{cases} R=\sqrt{2} \\ tan\phi=1 \Rightarrow \phi = \pi/4 \end{cases}\) \(cosx+sinx=\sqrt{2}.cos(x+\pi/4)\) |
Formules de développement
cosa.cosb
|
Connaissances pour la démonstration:
En additionnant les 2 équations ci-dessus, on obtient: \(cos(a-b)+cos(a+b)=2.cosa.cosb\) Et donc en divisant a droite et a gauche par 2, il vient: \[\boxed{ cosa.cosb=\frac{cos(a-b)+cos(a+b)}{2}}\]
En particulier, si \(a=b\), on retrouve \(cos²a=\frac{1+cos(2a)}{2}\), une formule de multiplication des angles |
sina.sinb
|
Connaissances pour la démonstration:
En soustrayant les 2 équations ci-dessus, on obtient: \(2.sina.sinb=cos(a-b)-cos(a+b)\) Et donc en divisant par 2 à droite et à gauche, il vient: \[\boxed{sina.sinb=\frac{cos(a-b)-cos(a+b)}{2}} \]
En particulier, si \(a=b\), on retrouve \(sin²a=\frac{1-cos(2a)}{2}\), une formule de multiplication des angles |
sina.cosb
|
Connaissances pour la démonstration:
En additionnant les 2 équations ci-dessus, on obtient: \(sin(a+b)+sin(a-b) = 2sina.cosb\) \[\boxed{sina.sinb=\frac{sin(a+b)+sin(a-b)}{2}}\] |
Résumé
| \[\boxed{ cosa.cosb=\frac{cos(a-b)+cos(a+b)}{2} \\ sina.sinb=\frac{cos(a-b)-cos(a+b)}{2} \\ sina.sinb=\frac{sin(a+b)+sin(a-b)}{2}}\] |
Angles supplémentaire, complémentaire et opposé
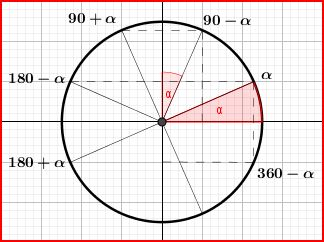
Dessinons maintenant le cercle unité avec plusieurs angles remarquables (\(\pi = 180°\)):
Ne pas hésiter à redessiner ce cercle trigonométrique, ou à se le remémorer, le visualiser, à chaque fois que vous en aurez besoin lors des exercices et devoirs.
|
\[-\alpha\] |
\[ cos(-\alpha)=cos(\alpha)\] paire |
\[sin (-\alpha)=-sin(\alpha) \] impaire |
|
|
\[\alpha + 2k\pi\] |
\[ cos(\alpha+ 2k\pi)=cos(\alpha)\] \(2\pi\) périodique |
\[sin (\alpha+ 2k\pi)=sin(\alpha) \] \(2\pi\) périodique |
|
| \[\pi-\alpha\] |
\[ cos(\pi-\alpha)=-cos(\alpha)\] |
\[sin (\pi-\alpha)=sin(\alpha)\] | |
| \[\pi+\alpha\] | \[ cos(\pi+\alpha)=-cos(\alpha)\] | \[sin (\pi+\alpha)=-sin(\alpha)\] | |
| \[\frac{\pi}{2}+\alpha\] | \[cos(\frac{\pi}{2}+\alpha)=-sin(\alpha)\] | \[sin(\frac{\pi}{2}+ \alpha)=cos(\alpha)\] | |
| \[\frac{\pi}{2}-\alpha\] | \[cos(\frac{\pi}{2}-\alpha)=sin(\alpha)\] | \[sin(\frac{\pi}{2} - \alpha)= cos(\alpha)\] |
Ces formules se retiennent facilement à condition de bien mémoriser la figure ci dessus avec les angles.
Elles ne seront alors pas reprises dans le précis de trigonométrie en fin de chapitre.
Identité Remarquable Trigonométrique
Identité remarquable
|
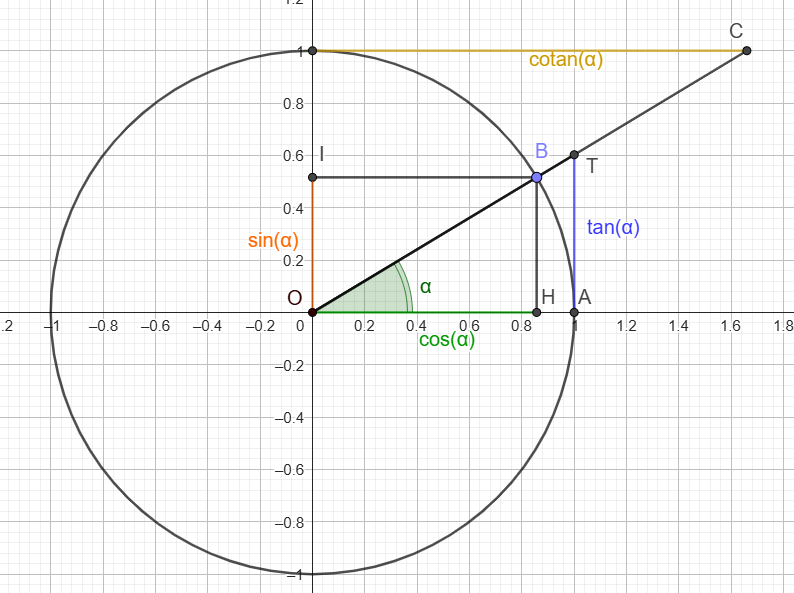
Appliquons le Théorème de Pythagore dans le triangle (OHB). Alors:
Et pour finir: \[\boxed{ \begin{align*} cos²\alpha + sin²\alpha = 1 \end{align*}}\]
|
|
tan² en fonction de cos² et sec²
|
Connaissances:
En divisant l'identité remarquable par \(cos²\alpha\) des 2 côtés: \(\begin{align*}1+\frac{sin²\alpha}{cos²\alpha}=\frac{1}{cos²\alpha} \Leftrightarrow 1+tan²\alpha=\frac{1}{cos²\alpha}=sec²\alpha \end{align*}\) |
\[\boxed{1+tan²\alpha=\frac{1}{cos²\alpha}}\] |
cotan² en fonction de sin² et csc²
|
Connaissances:
En divisant l'identité remarquable par \(sin²\alpha\) des 2 côtés: \(\begin{align*}\frac{cos²\alpha}{sin²\alpha}+1=\frac{1}{sin²\alpha} \Leftrightarrow 1+cotan²\alpha=\frac{1}{sin²\alpha}=csc²\alpha \end{align*}\) |
\[\boxed{1+cotan²\alpha=\frac{1}{sin²\alpha}}\] |