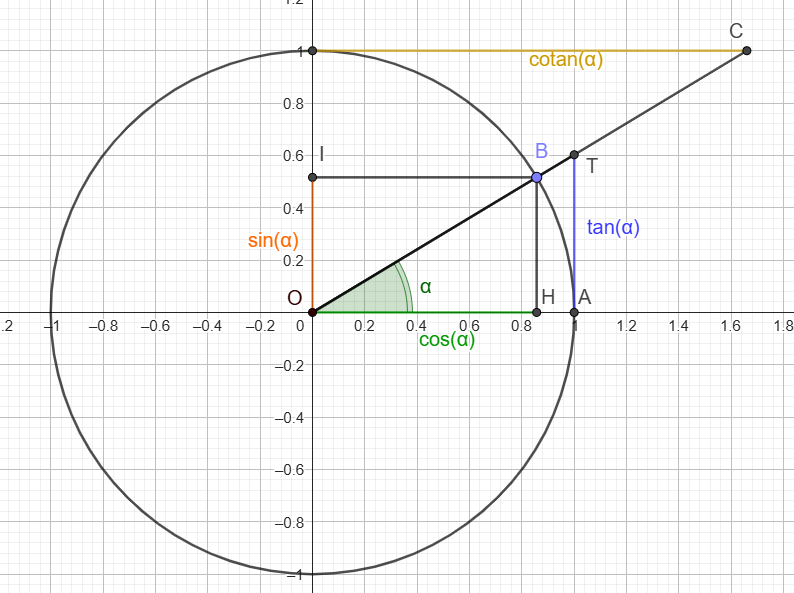
Soit un cercle de rayon r = 1 (OA=OB=1)  autrement appelé Cercle Unité ou Cercle Trigonométrique, et B un point situé sur ce cercle (OB=1).
Vous pouvez cliquer sur l'image pour ouvrir une fenêtre et bouger le point B pour voir ce qui se passe.

On définit:

• \(cos\alpha\): projection orthogonale du segment OB sur l'axe des abscisses: soit OH
• \(sin\alpha\): projection orthogonale du segment OB sur l'axe des ordonnées: soit OI
• \(tan\alpha\): projection de B depuis O sur la droite tangente au cercle unité en A: soit AT

Ce qui donne les définitions mathématiques suivantes avec OA=OB=1:

\[\boxed{cos\alpha=OH = \frac{OH}{OB} \space \space ; \space \space     sin\alpha=OI= \frac{OI}{OB} = \frac{HB}{OB}  \space \space ; \space \space  tan\alpha = \frac{AT}{OA}}\]

• Le triangle (OAT) est rectangle en A
• Le triangle (OHB) est rectangle en H
• Donc dans le triangle (OAT) les droite HB et AT sont parallèles

En appliquant le Théorème de Thalès , nous pouvons écrire :

\[\boxed{tan\alpha=\frac{AT}{OA}=\frac{HB}{OH}=\frac{sin\alpha}{cos\alpha}}\]

On pourrait aussi définir ces fonctions trigonométriques par les côtés des triangles rectangles:

• Sin = cote Opposé (à l'angle) sur Hypothènue
• Cos = côté Adjascent (à l'angle) sur Hypothénuse
• Tan = côté Opposé (à l'angle) sur côté Adjascent (à l'angle)

Il vient tout naturellement le moyen mnémotechnique suivant : SOH-CAH-TOA
Ou encore pour les loubards : CAH SOH TOA ( casse toi !!!!!!!!)

\[\boxed{\text{SOH-CAH-TOA} \\ \text{CAH-SOH-TOA}}\]

Ces fonctions sont utilisées surtout par les anglosaxons. Pour autant, en connaissant les dérivées et primitives de ces fonctions trigonométriques, certains problèmes peuvent devenir plus faciles.

\[\boxed{\text{cotangente: } cotan(\alpha)=\frac{1}{tan\alpha} \\ \text{secante: } sec(\alpha)=\frac{1}{cos\alpha} \\ \text{cosecante: }  csc(\alpha)= \frac{1}{sin\alpha}}\]

\(\begin{cases}e^{ix}=cosx+i.sinx  \\ e^{-ix}=cosx-i.sinx \end{cases} \)

En additionnant les 2 expressions: \(e^{ix}+e^{-ix}= 2 cosx \Leftrightarrow cosx=\frac{e^x+ e^{-x}}{2}\)

En soustrayant les 2 expressions: \(e^{ix}-e^{-ix}= 2.i.sinx \Leftrightarrow sinx=\frac{e^x- e^{-x}}{2.i}\) 

\[\boxed{\begin{align*}cosx=\frac{e^x+ e^{-x}}{2} && sinx=\frac{e^x- e^{-x}}{2.i} \end{align*}}\]