|
\(\begin{align*} I & = \int \sqrt{(x²+4x+13)}.dx \end{align*}\)
Nous avons ici un polynome du 2nd degré non factorisable sous un radical. Notre chance de nous en sortir est d'aller chercher une forme en \( tan²x + 1 = sec²x \), ce qui nous permettra de retirer le radical.
A réaliser :
- factoriser et se ramener a une forme \(u²+1\)
- faire un changement de variable
- \(tan\theta=u\) et revenir a une forme en \(x\)
Ici nous avons presua un carré parfait avec \(x²+4x+........\). Alors écrivons que \(x²+4x=(x+2)²-4\)
\(\begin{align*}
I & =\int \sqrt{[(x+2)²-4+13]}.dx = \int \sqrt{[(x+2)²+9]}.dx\\
& = \int \sqrt{[(x+2)²+3²]}.dx = \int \sqrt{9[(\frac{(x+2)²}{9}+\frac{9}{9}]}dx \\
& = \int 3 \sqrt{(\frac{x+2}{3})²+1}dx = 3 \int \sqrt{(\frac{x+2}{3})²+1}dx
\end{align*}\)
Procédons maintenant à un changement de variable de façon a retrouver une forme en \(tan²x +1\) et retrouver ensuite \(sec²x\):
\( \begin{align*} & \begin{cases} tan \theta=\frac {x+2}{3} \Rightarrow 3.tan \theta = x+2 \\ dx= 3sec² \theta .d \theta\end{cases} \\ \\
I & =3 \int \sqrt{tan² \theta+1} \times 3sec² \theta .d \theta \\
& = \int 9 \sqrt{sec² \theta} sec² \theta .d \theta \\
& = 9 \int sec^{3} \theta .d \theta \\
& = 9 \big[ \frac{1}{2} (sec \theta . tan \theta + ln \lvert sec \theta+ tan \theta \rvert) \big] +C \\
& = \frac{9}{2} \big[ (sec \theta . tan \theta + ln \lvert sec \theta+ tan \theta \rvert) \big] +C
\end{align*}\)
Cette dernière ligne trouve sa justification dans l'exercice 24.
Revenons maintenant à la variable \(x\), et commençons par un petit schéma: nous avons \(tan \theta = \frac{x+2}{3}\) qui nous permet de dessiner un triangle rectangle dont nous connaissons les 3 côtés.
Dans ce triangle rectangle, il sera possible de retrouver les differentes fonctions trigonométriques dont nous auront besoin pour trouver \(I\) et terminer l'exercice.
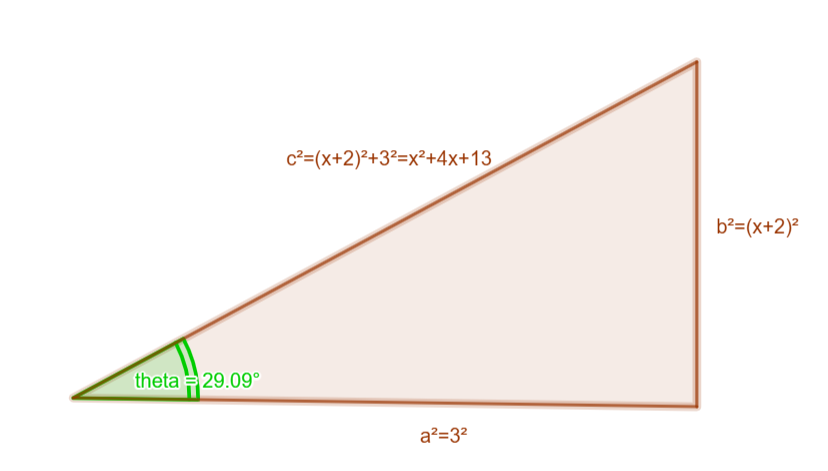
\( \begin{align*}
I & = \frac{9}{2} \big[ (sec \theta . tan \theta + ln \lvert sec \theta+ tan \theta \rvert) \big] +C \\
& \text{Avec: } \begin{cases} sec\theta = \frac{1}{cos\theta} = \frac{\sqrt{x²+4x+13}}{3} \\ tan\theta = \frac{x+2}{3}\end{cases} \\ \\
I & = \frac{\cancel{9}}{2} \frac{\sqrt{x²+4x+13}}{\cancel{3}}.\frac{x+2}{\cancel{3}} + \frac{9}{2} ln \bigg\lvert \frac{\sqrt{x²+4x+13}}{3}+\frac{x+2}{3} \bigg\rvert + C_1 \end{align*}\)
D'après le schéma ci dessus et parce qu'on est dans un triangle rectangle, on a:
\( \begin{align*} \forall x: \sqrt{x²+4x+13} \geq x+2 \end{align*}\)
On peut donc retirer les valeurs absolues.
\( \begin{align*}I & = \frac{1}{2}(x+2)\sqrt{x²+4x+13}+\frac{9}{2}ln \frac{1}{3} \bigg[\sqrt{x²+4x+13}+(x+2) \bigg] + C_1\\
& = \frac{1}{2}(x+2)\sqrt{x²+4x+13}+\frac{9}{2} \bigg[\cancel {ln \frac{1}{3}}^{=cte} + ln \bigg[\sqrt{x²+4x+13}+(x+2)\bigg] \bigg] + C_1 \\
& = \frac{1}{2}(x+2)\sqrt{x²+4x+13} + \frac{9}{2}ln \bigg[\sqrt{x²+4x+13}+(x+2)\bigg] + C_2
\end{align*}\)
\[\boxed{I = \frac{1}{2}(x+2)\sqrt{x²+4x+13} + \frac{9}{2}ln \bigg[ \sqrt{x²+4x+13}+(x+2) \bigg] + C_2 \in \mathbb R}\]
|

