|
\( \begin{align*} I & = \int sec^{-1}x.dx \end{align*}\)
Procédons à une IPP
| |
D |
|
I |
| \(+\) |
\(sec^{-1}x\) |
|
\(1\) |
| |
|
\(\searrow\) |
|
| \(-\) |
\(\frac{1}{x \sqrt{x²-1}}\) |
\(\rightarrow\) |
\(x\) |
\( \begin{align*} I & = x.sec^{-1}x - \int \frac{x}{x \sqrt{x²-1}}.dx \\
& = x.sec^{-1}x - \int \frac{1}{ \sqrt{x²-1}}.dx \\
& x = sec \theta \Rightarrow dx= sec \theta . tan \theta . d\theta \\
I & = x.sec^{-1}x- \int \frac{1}{\sqrt{sec²\theta}-1}sec \theta . tan \theta . d\theta \\
& = x.sec^{-1}x- \int \frac{1}{\sqrt{tan²\theta}}sec \theta . tan \theta . d\theta \\
& = x.sec^{-1}x- \int \frac{1}{tan \theta}sec \theta . tan \theta . d\theta \\
& = x.sec^{-1}x- \int sec \theta . d\theta \\
& = x.sec^{-1}x- ln \lvert sec \theta + tan \theta \rvert+ C \\
\end{align*}\)
\( \begin{align*} \begin{cases} x = sec \theta \Rightarrow cos \theta = \frac{1}{x} \\
tan \theta = \sqrt{x²-1} \end{cases} \\ \\
I = x.sec^{-1}x- ln \lvert x + \sqrt{x²-1} \rvert+ C\end{align*}\)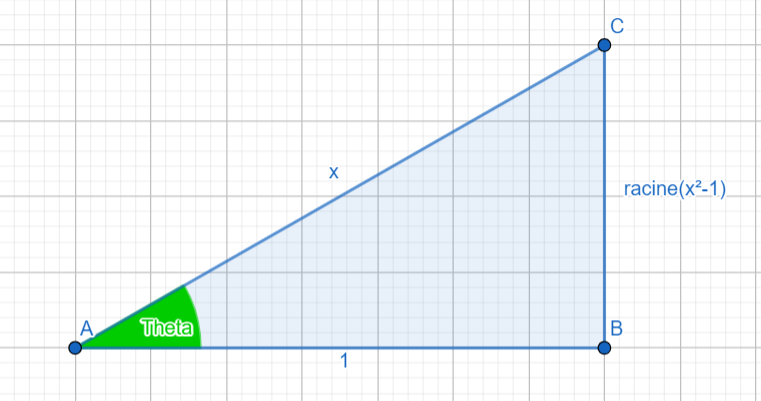
\[\boxed {\begin{align*}I = x.sec^{-1}x- ln \lvert x + \sqrt{x²-1} \rvert+ C(\in \mathbb R) \end{align*}}\]
|

