Exponentielle

 

1 - Au Lycée

Définition 1:
Il existe une unique fonction \(f\) dérivable sur \(\mathbb R\) telle que \(f'=f\) et \(f(0) = 1\). Cette fonction est appelée fonction exponentielle. On la note \(exp(x)\) ou \(e^x\).

 

Propriétés algébrique :

\(\forall x \in \mathbb R\) et \(\forall y \in \mathbb R\), \(\forall k \in \mathbb Z\)

  • \(e^x \gt 0\)
  • \(e^0=1\)
  • \(e^x \times e^{-x} = 1\)
  • \(e^{x+y}=e^x \times e^y\)
  • \(e^{x-y}=\frac{e^x}{e^y}\)
  • \(e^{-x}= \frac{1}{e^x}\)
  • \(\big( e^x)^k=e^{kx}\)

 

Sens de variation :
  • la fonction \(x \mapsto e^x\) est est dérivable sur \(\mathbb R\) et \(\big[ e^x \big]' = e^x \space \gt 0\)
  • En conséquence, la fonction \(x \mapsto e^x\) est strictement croissante sur \(\mathbb R\)

 

Dérivée et primitives:

Soit \(u\) une fonction dérivable sur un intervalle \(I\) et \(g\) la fonction définie par \(g(x) = e^{u(x)}\)

  • La fonction \(g\) est dérivable sur \(I\) et, \(\forall x \in I, g'(x) = u'(x)e^{u(x)}\)
  • Une primitive de \(u'(x)e^{u(x)}\) est \(e^{u(x)}\)

 

Limites:
  • \(\begin{align*} \lim_{x \to +\infty} e^x=+\infty \end{align*}\)
  • \(\begin{align*} \lim_{x \to -\infty} e^x=0 \end{align*}\)
  • \(\begin{align*} \lim_{x \to +\infty} \frac{e^x}{x}=+\infty \end{align*}\)
  • \(\begin{align*} \lim_{x \to -\infty}x e^x=0 \end{align*}\)
  • \(\begin{align*} \lim_{x \to 0} \frac{e^x-1}{x} =1 \end{align*}\)

 

Notation:
  • \(e^1 \approx 2.718\)

 

Représentation graphique:

 

2 - En post bac

On suppose connu les propriétés suivantes:

  • Toute fonction réelle \(f\) continue sur un intervalle \(I\) admet une primitive \(F: I \mapsto \mathbb R\) telle que \(F'=f\)
  • 2 primitives de \(f\) différent d'une constante
  • si \( f: I \mapsto \mathbb R\) est une fonction dérivable, avec une dérivée de signe fixe et qui ne s'annule qu'un nombre fini de fois, alors \(f\) définit une bijection de \(I\) sur l'intervalle \(J=f(I)\) 
  • Si \(f\) est  monotone sur \(I\), alors, a chaque extrémité de \(I\), la fonction \(f\) admet une limite , finie ou infinie
 

La définition vue en post bac est quelque peu différente.

Définition:
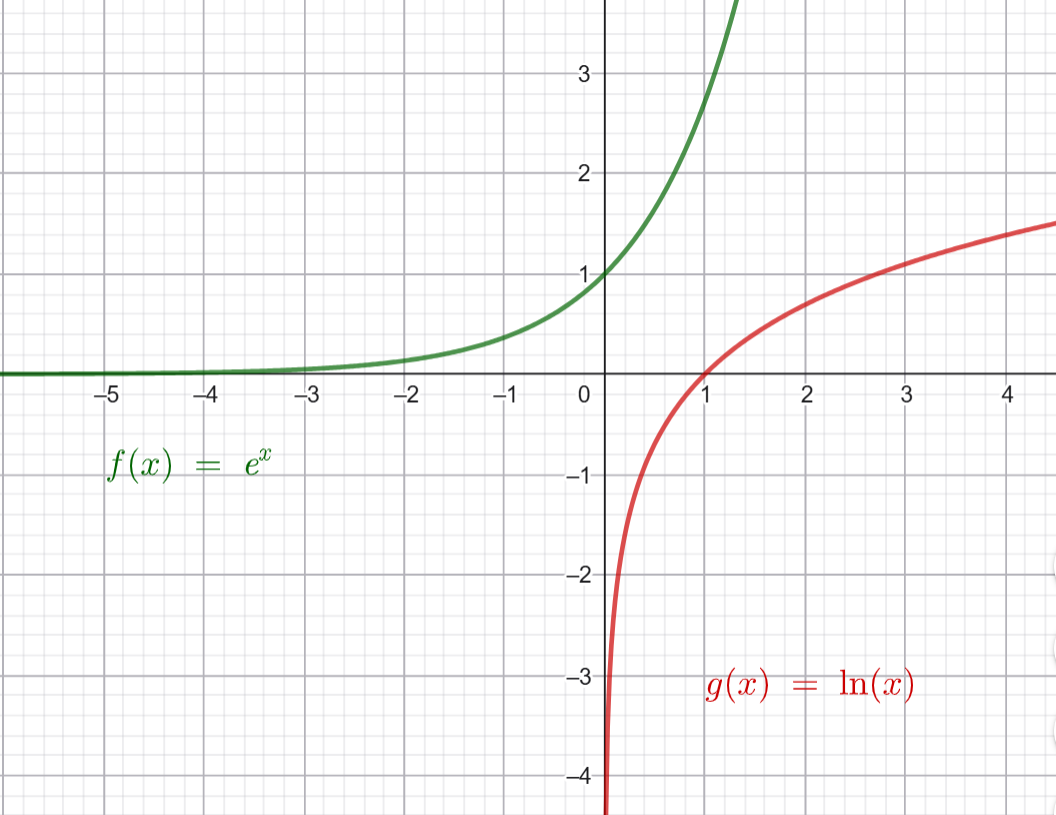
La fonction exponentielle, notée \(exp(x)\) ou \(e^x\), est la fonction réciproque de la fonction logarithme népérien.
 
Proposition:

La fonction exponentielle est une bijection strictement croissante de \(\mathbb R\) dans \(\mathbb R_+^*\), vérifiant \(e^0=1\) ainsi que :  

\(\begin{align*} \lim_{x \to -\infty} e^x=0 \end{align*}\) et \(\begin{align*} \lim_{x \to -\infty} e^x=0 \end{align*}\)

Elle est dérivable sur \(\mathbb R\) et on a \(\big[ e^x \big]'=e^x\)

 

Proposition:
Pour \(x \in \mathbb R\), on a \(1+x \leq e^x\), avec égalité si, et seulement si \(x=0\)