Exercice 40
\( \begin{align*} \int_1^2 \sqrt{x²-1}dx \end{align*}\) |
Connaissances:
- trigonométrie hyperbolique
|
\( \begin{align*} \end{align*}\)
|
Exercice 39
\(\begin{align*}\int\frac{1}{(x²+4)²}dx \end{align*}\) |
Connaissances:
- changement de variable
- une forme \(u²+a²\) au dénominateur implique un changement de variable \(u = a.tan \theta\)
- trigonométrie
- trigonométrie et notation anglosaxonne
- exprimer \(\theta\), \( sin \theta\) et \(cos \theta\) en fonction de \(x\)
|
\(\begin{align*}I & = \int\frac{1}{(x²+4)²}dx \\ Nous avons en bas une forme en \(u²+a²\). ceci nous indique d aller vers un changement de variable trigonométrique du style \(u=tan \theta\). En posant même \(u=2tan \theta\) nous pourrons factoriser par \(2\) et retrouver du \(1+tan² \theta\) que nous saurons gérer. \(\begin{align*} & \begin{cases} x=2tan \theta \\ dx = 2(1+tan² \theta) d \theta\end{cases} \Rightarrow \begin{cases} \theta=tan^{-1}(x/2) \\ dx = 2(sec² \theta) d \theta\end{cases} \\ Il faut maintenant diminuer la puissance de \(cos \theta\) puis primitiver: \(\begin{align*}I & =\frac{1}{8} \int cos² \theta d\theta \\ Comme nous avons \(\theta\), \(sin \theta\), et \(cos \theta\), il est plus facile de dessiner un triangle rectangle pour retrouver ces valeurs en fonction de \(x\)
Il suffit maintenant de remplacer \(\theta\), \(sin \theta\), et \(cos \theta\) par leur valeur pour trouver \(I\) \(\begin{align*}I & = \frac{1}{16} \bigg[ tan^{-1}(x/2) + \frac{x}{\sqrt{x²+2²}}.\frac{2}{\sqrt{x²+2²}} \bigg] +C \\ \[ \boxed{ \begin{align*}I = \frac{1}{16} \bigg[ tan^{-1}(x/2) + \frac{2x}{\sqrt{x²+2²}} \bigg] +C(\in \mathbb R) |
Exercice 38
\(\begin{align*}\int x² \sqrt[3]{1+x^3}dx \end{align*}\) |
Connaissances:
- changement de variable
- primitive de fonction polynome
- calculs avec des puissance \(a/b\)
|
\(\begin{align*}I & = \int x² \sqrt[3]{1+x^3}dx \end{align*}\) On remarque que \((1+x^3)'=3x²\) et on a alors le produit d'une dérivée et d'une fonction composée. Cela nous oriente vers un changement de variable: \(\begin{align*} & \begin{cases} u=1+x^3 \\ du=3x².dx\end{cases} \\ \[ \boxed{ \begin{align*} I & = \frac{1}{4} (1+x^3) \sqrt[3]{1+x^3} + C(\in \mathbb R) \end{align*}}\] |
Exercice 37
\(\begin{align*}\int x^3sin(2x)dx \end{align*}\) |
Connaissances:
- primitive ou dérivée de fonction polynome
- primitive ou dérivée de fonction trigonométriques
- intégration par parties
|
\(\begin{align*}I & = \int x^3sin(2x)dx \end{align*}\) Nous avons ici le produit de 2 fonctions facilement dérivables ou primitivables, ce qui nous conduit à essayer une intégration par parties. Etant donné le degré du polynome, il nous faudra plusieurs intégrations successives:
\(\begin{align*}I & = \int x^3sin(2x)dx \\ \[\boxed{\begin{align*}I & = -\frac{1}{2}x^3cos(2x)+\frac{3}{4}x²sin(2x)+\frac{3}{4}x.cos(2x)-\frac{3}{8}sin(2x) +C(\in \mathbb R) \end{align*}}\] |
Exercice 35
\(\begin{align*} \int \frac{1}{e^x+e^{-x}}dx \end{align*}\) |
Connaissances:
- exponentielles
- changement de variable
- primitive de \(\frac{1}{x²+1}=tan^{-1}x\)
|
\(\begin{align*} I & = \int \frac{1}{e^x+e^{-x}}dx \\ Posons le changement de variable \(u =e^x\) \(\begin{align*} & \begin{cases} u = e^x \\ du = e^x dx \end{cases} \\ \[ \boxed{\begin{align*} I = tan^{-1}(e^x)+C (\in \mathbb R)\end{align*}}\] |

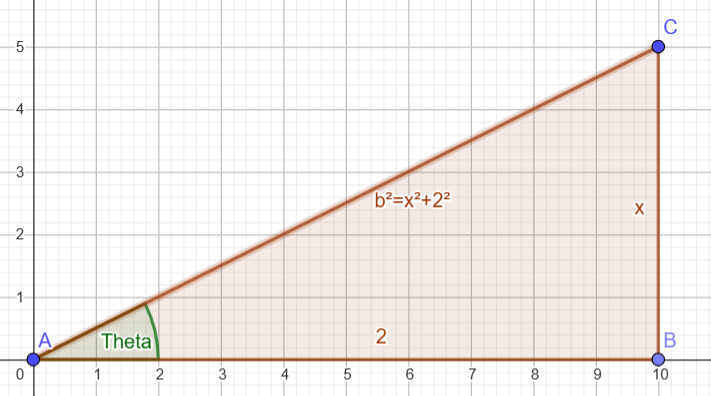 \(\begin{align*} & \theta=tan^{-1}(x/2) \Rightarrow \begin{cases} \text{Hypoténuse } = \sqrt{x²+2²} \\ \\ sin \theta = \frac{x}{\sqrt{x²+2²}} \\ cos \theta = \frac{2}{\sqrt{x²+2²}} \end{cases} \end{align*}\)
\(\begin{align*} & \theta=tan^{-1}(x/2) \Rightarrow \begin{cases} \text{Hypoténuse } = \sqrt{x²+2²} \\ \\ sin \theta = \frac{x}{\sqrt{x²+2²}} \\ cos \theta = \frac{2}{\sqrt{x²+2²}} \end{cases} \end{align*}\)