Exercice 60
\(\begin{align*} \int_{-1}^1 \sqrt{4-x²}.dx \end{align*}\) |
Connaissances:
- Intégrale d'une fonction paire
- Equation d'un cercle
- surface d'un triangle
- les angles dans un triangle
- surface d'un secteur de rayon \(r\) et d'angle \(\theta\)
|
\( \begin{align*} I & = \int_{-1}^1 \sqrt{4-x²}.dx \end{align*}\) Remarque: l'intégrande est une fonction paire: \(\begin{align*}I & = \int_{-1}^1 \sqrt{4-x²}.dx \\ Résolution par raisonnement géométrique (faire le dessin):
On en déduit la surface totale : \(\begin{align*}I & = 2 \times \text{(surface du triangle + surface de la part de pizza)} \\ \[\boxed {\begin{align*} I =\sqrt 3 + 2\pi/3 \end{align*}}\] |
Exercice 59
\(\begin{align*} \int x² \sqrt{x+4}.dx \end{align*}\) |
Connaissances:
- Changement de variable
- Primitives de polynômes
|
\( \begin{align*} I & = \int x² \sqrt{x+4}.dx \end{align*}\) Faisons le changement de variable \(u=x+4 \Rightarrow dx=du\) \(\begin{align*}I & = \int x² \sqrt{x+4}.dx \\
\[\boxed {\begin{align*} I =\frac{2}{7}(x+4)^{7/2}- \frac{16}{5}(x+4)^{5/2}+\frac{32}{3}(x+4)^{3/2} +C (\in \mathbb R) \end{align*}}\] |
Exercice 58
\(\begin{align*} \int \frac{1-cosx}{1+cosx}.dx \end{align*}\) |
Connaissances:
- trigonométrie
- Trigonométrie notation anglosaxonne
|
\( \begin{align*} I & = \int \frac{1-cosx}{1+cosx}.dx \end{align*}\) On pourrait multiplier numérateur et dénominateur par le conjugué du dénominateur , cela fonctionnerait. Je vous propose ici une méthode plus rapide:
\( \begin{align*} I & = \int \frac{1-cosx}{1+cosx}.dx \\
\[\boxed {\begin{align*} I =2tan\frac{x}{2} - x + C(\in \mathbb R) \end{align*}}\] |
Exercice 57
\(\begin{align*} \int sec^{-1}x.dx \end{align*}\) |
Connaissances:
- trigonométrie
- Trigonométrie notation anglosaxonne
- Intégration par partie
- Changement de variable
|
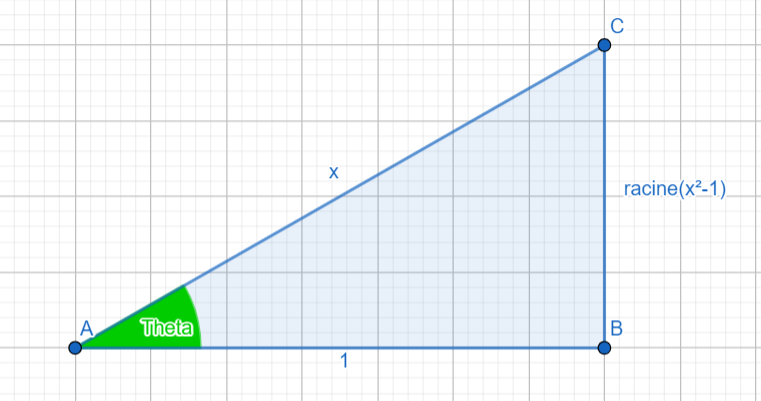
\( \begin{align*} I & = \int sec^{-1}x.dx \end{align*}\) Procédons à une IPP
\( \begin{align*} \begin{cases} x = sec \theta \Rightarrow cos \theta = \frac{1}{x} \\
\[\boxed {\begin{align*}I = x.sec^{-1}x- ln \lvert x + \sqrt{x²-1} \rvert+ C(\in \mathbb R) \end{align*}}\] |
||||||||||||||||
Exercice 56
\(\begin{align*} \int x.secx.tanx.dx \end{align*}\) |
Connaissances:
- trigonométrie
- Trigonométrie notation anglosaxonne
- Intégration par partie
|
\( \begin{align*} I & = \int x.secx.tanx.dx \end{align*}\) Procédons à une IPP
\[\boxed {\begin{align*} I =x.secx - ln \lvert secx+tanx \rvert +C(\in \mathbb R) \end{align*}}\] |
||||||||||||||||||||||||