Primitives usuelles
Dans ce chapitre :
- les primitives des fonctions usuelles
- les formes remarquables
- quelques exemples
1 - Primitives des fonctions usuelles
|
Certaines fonctions sont vues à partir de la classe de Terminale et d'autres en Post-Bac
|
2 - Formes remarquables
|
Soit \(u\) , une fonction:
|
3 - Exemples
3-1 \(u'u^n\)
3-2 \(u'/u\)
3-3 \(u'lnu\)
3-4 \(u'e^u\)
3-5 \(\frac{u'}{\sqrt u}\)
3-6 \(u'sinu\)
Le même genre d'intégration peut être faite avec des fonctions
3-7 \(u'tanu\)
Il en va de même avec
3-8 \(u'tanu\)
Il en va de même avec
|
||||||||||||||||||||||||||||||||
Primitives
Pour toute cette partie, \(I\) est un intervalle d'intérieur non vide. Les fonctions considérées sont à valeurs dans \(\mathbb K\). (\(\mathbb K\) est l'ensemble des réels \(\mathbb R\) ou des complexes \(\mathbb C\))
1- Généralités
Définition:
Par exemple de \(F(x) = x²\) est une primitive de de \(f(x)= 2x\). En effet, \(F'(x) = (x²)'=2x = f(x)\) Remarque:
Propriété:
En effet, si \(\forall x \in \mathbb R, F(x) = C\), alors \(F'(x)=0=f(x)\)
Théorème:
Propriétés:
Par exemple:
Remarque: Pour déterminer toutes les primitives d'une fonction, il suffit d'en trouver une. Toutes les autres s 'en déduisent à une constante près.
Proposition:
Remarque importante :De nombreux calculs de primitives se font en reconnaissant la dérivée d'une fonction composée. Par exemple: |
2 - Existence de primitive
|
Le théorème suivant permet :
Ce théorème est connu sous le nom de Théorème fondamental de l'analyse \[ \begin{align*} \int_a^b f(t)dt = \int_a^b (\Re f(t)) dt + \int_a^b (\Im f(t))dt \end{align*}\]
Théorème:
Proposition:
Remarque: Soit \(f\) une fonction continue sur \(I\) et \(a \in I\). Les primitives de \(f\) sur \(I\) sont donc les fonctions |
Primitives usuelles vues en classe de Terminale
Soient:
- \(C \in \mathbb R\)
- \(n \in \mathbb N\)
- \(a,b \in \mathbb R²\) avec \(a \neq 0\)
|
Primitives et Intégrales
Dès l’Antiquité le problème du calcul de grandeurs est posé (aire d’une surface, longueur d’une courbe) est posé.
Archimède développe la méthode d’exhaustion: il approche l’aire délimitée par un arc de parabole à l’aide d’aires géométriques simples.
Cette méthode restera la seule connue pendant 20 siècles!
Au 17ième siècle, l’invention du calcul infinitésimal permet de nouvelles avancées. A l’origine le calcul intégral est développé par Leibniz (1646-1716) et Newton (indépendamment l’un de l’autre).
Désormais l’intégration est vue comme un problème inverse de la dérivation. Cette approche est poursuivie par de nombreux mathématiciens pendant deux siècles.
La formalisation arrive avec
- la célèbre intégrale de Riemann (1826-1866), mathématicien allemand, à l’origine des développements ultérieurs de la théorie, et
- l’intégrale de Lebesgue au début du 20ième siècle.
L’intégration est encore un sujet de recherche contemporain
Les intégrales de Wallis - 2
Sujet
Partie A :\[\forall n \in \mathbb N, I_n = \int_0^{\pi/2} cos^nt.dt\]
Partie B:Pour la suite, on pose:\[\forall n \in \mathbb N, \forall x \in ]-\pi/2;\pi/2[, F_n(x)=\int_0^xtan^nt.dt\]
|
Partie A
0 - Préliminaires
|
\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(cost)^n dt\end{align*}\)
|
1 - Etudier la monotonie de la suite \((I_n)_{(n \in \mathbb N)}\)
|
Sur \([0; \pi/2]\), la fonction \( t \mapsto cos(t)\) est:
La suite \((I_n)_{(n \in \mathbb N)}\) est décroissante et \(I_n >0\) |
2-1 Calculer \(I_0\)
|
\(\begin{align*}I_0 & = \int_0^{\pi/2}cos^nt.dt \[ \boxed{I_0 = \pi/2}\] |
2-2 Calculer \(I_1\)
|
\(\begin{align*}I_1 & = \int_0^{\pi/2}cos^nt.dt = \int_0^{\pi/2}cos^1t.dt \\ \[ \boxed{I_1 = 1}\] |
3 - Démontrer à l'aide d'une IPP que \(\forall n \in \mathbb N\), \((n+2)I_{n+2}= (n+1)I_n\)
|
\(\forall n \in \mathbb N\), \(\begin{align*}I_{n+2} & = \int_0^{\pi/2}cos^{n+2}t.dt \\ \[\boxed{\forall n \in \mathbb N, (n+2)I_{n+2}= (n+1)I_n}\] |
4 - En déduire que \(\forall n \in \mathbb N, (n+1)I_{n+1}I_n = \pi/2 \)
|
Soit \(U_n\) telle que \( \forall n \in \mathbb N, U_n= (n+1)I_{n+1}I_n\) \(\begin{align*} U_{n+1} & = (n+2)I_{n+2}I_{n+1} \\ \(\begin{align*}\forall n \in \mathbb N, U_{n+1}= U_n \end{align*}\) donc la suite \(U_n\) est constante et : \[\boxed{\forall n \in \mathbb N, (n+1)I_{n+1}I_n = \pi/2} \] |
5 - Démontrer en utilisant les questions 1 et 3 que \(\lim\limits_{n \mapsto + \infty}\frac{I_{n-1}}{I_n}=1\)
On en déduit que \(\frac{n}{(n-1)} \leq \frac{I_{n-1}}{I_{n}} \leq 1\) Or \(\lim\limits_{n \to + \infty}\frac{n}{n-1}=1\) et par le Théorème des gendarmes, on obtient: \[\boxed {\lim\limits_{n \mapsto + \infty}\frac{I_{n-1}}{I_n}=1}\] |
6-1 Démontrer que si \(n \to + \infty\) alors \(I_n\) à pour équivalent \( \sqrt{\frac{\pi}{2n}}\)
Il vient alors : \(\begin{align*} & (n+1) I_nI_{n+1} = \pi/2 \\ \[\boxed{I_n \space\space\widetilde{+\infty}\space\space {+ \infty} \sqrt{\frac{\pi}{2n}} }\] |
6-2 En déduire que la suite \(I_n\) converge et préciser sa limite
La suite \(I_n\) est décroissante et \(I_n>0\), et d'après le Théorème des suites monotones bornées: \(I_n\) converge. Comme \(I_n \space\space\widetilde{+\infty}\space\space \sqrt{\frac{\pi}{2n}}\) \(\lim\limits_{n \to + \infty}I_n=\lim\limits_{n \to + \infty}\sqrt{\frac{\pi}{2n}}=0\) \[ \boxed{I_n\text{ converge et }\lim\limits_{n \to + \infty}I_n=0}\] |
7-Démontrer que \(\begin{align*}\forall n \in \mathbb N, I_{2n} = \prod_{k=0}^{n-1}\frac{2k+1}{2k+2} \times \frac{\pi}{2} = \frac{(2n)!}{[2^n.n!]²}\frac{\pi}{2} \end{align*}\)
\(\begin{align*} \Leftrightarrow I_{nombre} & =\frac{nombre-1}{nombre} \times I_{nombre-2} \\ \[ \boxed{\begin{align*} \forall n \in \mathbb N, I_{2n} =\prod_{k=0}^{n-1} \frac{2k+1}{2k+2}\times \frac{\pi}{2} = \frac{(2n)!}{\big[ 2^n \times n!\big]^2} \frac{\pi}{2} \end{align*}}\] |
8-Déduire des questions 6 et 7 que \(\forall n \in \mathbb N, \lim\limits_{n \to + \infty}\frac{1 \times 3 \dots \times (2n+1)}{2 \times 4\times \dots \times 2n}\frac{1}{\sqrt n}=\frac{2}{\sqrt\pi}\)
|
Partie B
Pour la suite, on pose:
\[\forall n \in \mathbb N, \forall x \in ]-\pi/2;\pi/2[, F_n(x)=\int_0^xtan^nt.dt\]
0 - Préliminaires
|
\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} F_n(x)=\int_0^{x}tan^nt dt\end{align*}\)
|
1 - Calculer \(F_1(x)\) et \(F_2(x)\) \(\forall x \in ]-\pi/2;\pi/2[\)
|
\(\forall x \in ]-\pi/2;\pi/2[\), la fonction \(x \mapsto tan(x)\) est continue. Il en est de même pour la fonction \(x \mapsto tan^nx, \forall n \in \mathbb N\). En conséquence, \(\int_0^xtan^nt.dt\) existe. \[\boxed{\forall x \in ]-\pi/2;\pi/2[ \text{ et } \forall n \in \mathbb N, F_n(x) \text{ existe.} }\] \(\begin{align*}F_1(x) & =\int_0^xtan(t).dt \\ \[\boxed {\forall x \in ]-\pi/2;\pi/2[, F_1(x)=-ln(cos(x)) } \] \(\begin{align*}F_2(x) & =\int_0^xtan^2t.dt \[\boxed {\forall x \in ]-\pi/2;\pi/2[, F_2(x)= tan(x) -x }\] |
2 - Soient \(n \in \mathbb N,\) et \(x \in ]-\pi/2;\pi/2[\), démontrer que \(F_{n+2}(x)+F_n(x)=\frac{tan^{n+1}x}{n+1}\)
|
\(\forall n \in \mathbb{N^*}\) \( \begin{align*} F_{n+2}(x)+F_n(x) & = \int_0^xtan^{n+2}t.dt+\int_0^xtan^nt.dt \\ Pour \(n=0\) \(\begin{align*} F_2(x)+ F_0(x) & =\frac{tan^{0+1}x}{0+1}= tanx\end{align*}\) \(\begin{align*} F_2(x)+ F_0(x) & = \overbrace{tanx-x}^{F_2(x)} + \overbrace{ \int_0^xtan^0tdt}^{F_0(x)} \\ On en conclue que : \[\boxed {\forall n \in \mathbb N, \text{ et }\forall x \in ]-\pi/2;\pi/2[, F_{n+2}(x)+F_n(x) = \frac{tan^{n+1}x}{n+1} }\] |
3 - En déduire la valeur de \(F_4(x), \forall x \in ]-\pi/2;\pi/2[\)
|
\(\forall n \in \mathbb N, \text{ et } \forall x \in ]-\pi/2;\pi/2[, \) \(\begin{align*}& && F_{n+2}(x)+F_n(x) && = \frac{tan^{n+1}x}{n+1} \\ \[\boxed { \forall x \in ]-\pi/2;\pi/2[, F_4(x)=\frac{tan^{3}x}{3}-tan(x) +x }\] |
On pose: \(\begin{align*}\forall n \in \mathbb N, J_n=\int_0^{\pi/4}tan^nt.dt = F_n(\pi/4) \end{align*}\)
4 - Etudier la monotonie de \((J_n)_{n \in \mathbb N}\). \(J_n\) est elle convergente?
|
Pour \(x \in [0;\pi/4]\) on a \(\forall n \in \mathbb N\): \(\begin{align*} 0 & \leq tan x \leq 1 \\ Par positivité de l'intégrale, il vient \(J_{n+1} <J_{n}\)
\[\boxed{\begin{align*} \begin{cases} J_n \searrow \\ J_n \geq0 \end{cases} |
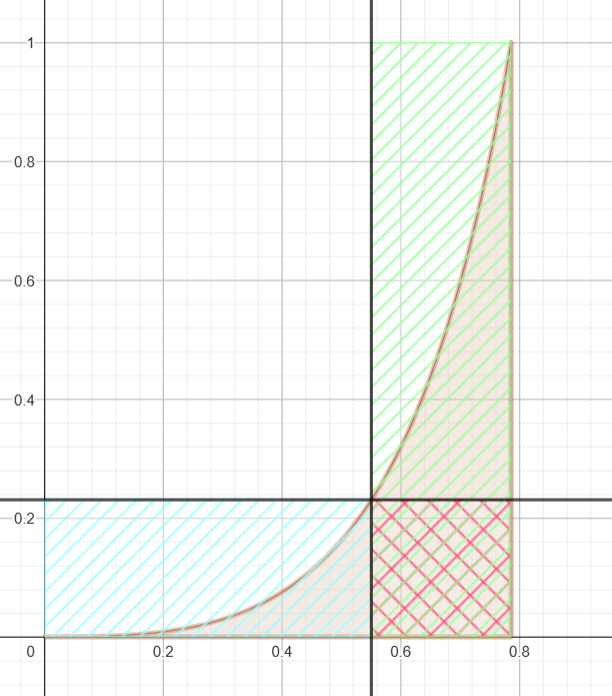
5 - Soit \(a \in ]0;\pi/4[\), montrer que\((\frac{\pi}{4}-a) tan^na \leq J_n \leq a.tan^na+(\frac{\pi}{4}-a)\)
|
Le sujet nous intime fortement de couper notre intégrale en 2 parties grace à la relation de Chasles. Il vient alors: \( \begin{align*}\int_0^{a} tan^nt.dt+ \int_a^{\pi/4} tan^nt.dt = J_n = \int_0^{a} tan^nt.dt +\int_a^{\pi/4} tan^nt.dt Plusieurs remarques: \( \forall n \in \mathbb N\)
\( \begin{align*} \overbrace{\int_0^{a} tan^nt.dt}^{>0}+ \int_a^{\pi/4} tan^nt.dt = & J_n = \underbrace{\overbrace{\int_0^{a} tan^nt.dt}^{\leq (a-0)tan^na}}_{\text{carré bleu}} +\underbrace{\overbrace{\int_a^{\pi/4} tan^nt.dt}^{(\pi/4-a)tan^n1}}_{\text{carré vert}} \\ Il vient : \[ \boxed { \begin{align*}\forall a \in ]0;\pi/4[, (\pi/4-a)tan^na \leq & J_n \leq a tan^n a +(\pi/4-a) \end{align*}}\] \(J_n\) prendra sa valeur si \( a \to \pi/4\) sans atteindre \(\pi/4\), et alors, Il résulte que :\(\lim (\pi/4-a)tan^na \leq \lim J_n \leq \lim a tan^n a +(\pi/4-a)\) avec \(\begin{align*} \begin{cases}\lim (\pi/4-a)tan^na=0 \\ Et par le Théorème des gendarmes : \[\boxed{\lim (J_n)_{n \in \mathbb N}=0}\] |
6 - On note \(\forall n \in \mathbb N , U_n=\frac{(-1)^n}{2n+1}\) et \((S_n)_{n \in \mathbb N}\) la suite des sommes partielles de \(U_n\)
6-1 - En utilisant la question Partie B - 2, montrer que , \(\forall n \in \mathbb N, S_n = \sum_{k=0}^n(-1)^k(J_{2k}+ J_{2k+2})\)
|
Rappels:
En conséquence: \(\begin{align*} \forall n \in \mathbb N, J_{2k+2}+ J_{2k}=\frac{tan^{2k+1}\pi/4}{2k+1} = \frac{1}{2k+1} \end{align*}\) Et \(\begin{align*} \forall n \in \mathbb N , U_n=\frac{(-1)^n}{2n+1} = (-1)^n(J_{2k+2}+ J_{2k}) \end{align*}\) On en conclue que \(\begin{align*} S_n = \sum_{k=0}^n U_n = \sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k})\end{align*}\)
\[ \boxed{\forall n \in \mathbb N, S_n =\sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k})}\] |
6-2 - En déduire que \(\forall n \in \mathbb N, S_n= \pi/4+(-1)^nJ_{2n+2}\)
|
\( \begin{align*}\forall n \in \mathbb N, S_n =\sum_{k=0}^n (-1)^n(J_{2k+2}+ J_{2k}) \end{align*}\) \(\begin{align*} & n = 0 && (-1)^0 (J_2+J_0) && = && \cancel{+J_2} &&+ J_0 \\ Avec: \(\begin{align*} J_0 = \int_0^{\pi/4}tan^0t.dt = \pi/4\end{align*}\) Et pour finir, on a: \[ \boxed {\forall n \in \mathbb N, S_n= \pi/4+(-1)^nJ_{2n+2}}\] |
6-3 - La série \(\sum U_n\) est elle convergente? Si oui quelle est sa somme?
| \( J_{2n+2} \) converge vers \(0\), en conséquence \(S_n\) converge vers \(\pi/4\) |
Les intégrales de Wallis - 1
Sujet
|
\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(sint)^n dt\end{align*}\)
|
0 - Préliminaires
|
\(\begin{align*}\forall n \in \mathbb N \end{align*}\), \(\begin{align*} I_n=\int_0^{\pi/2}(sint)^n dt\end{align*}\)
|
1 - Calculer \(I_0\) et \(I_1\)
|
\[\begin{align*} & I_n=\int_0^{\pi/2}sin^nt .dt \end{align*}\] \[\boxed{I_0=\pi/2 \text{ et } I_1=1}\] |
2 - Montrer que \((I_n)_{n \in \mathbb N}\) est bien définie
|
\[\begin{align*} & I_n=\int_0^{\pi/2}sin^nt .dt \end{align*}\] Il faut démontrer que chaque terme de la suite (\(I_0\), \(I_1\), \(I_2\), \(I_3\), \(\dots\), \(I_n\) \(\dots\)) existent. La fonction \(t \mapsto sin(t)\) est bien définie, continue et dérivable sur \(\mathbb R\), donc aussi sur l'intervalle sur \([0;\pi/2]\), et par conséquent la fonction \(t \mapsto sin^nt\) est bien définie, continue et dérivable sur \([0;\pi/2]\). L'intégrale de la fonction \(t \mapsto sin^nt\) est calculable quelque soit la valeur de n. Donc \(I_n\) est bien définie \(\forall n \in \mathbb N\) |
3 - Montrer que \(\forall n \in \mathbb N, I_n = \int_0^{\pi/2}(cost)^n dt \) et en déduire \(I_2\)
|
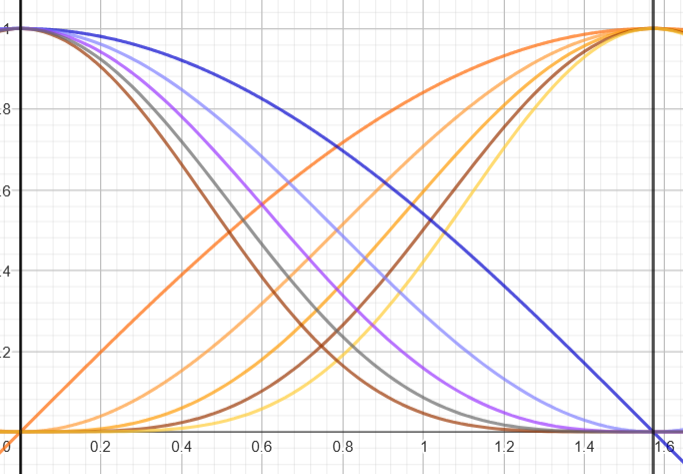
On peut essayer de tracer les fonctions \(sin^nt\) et \(cos^nt\) pour différentes valeurs de \(n\)
On observe immédiatement une symétrie / égalité de l'aire située sous les courbes \(sin^nt\) et \(cos^nt\). De façon générale, lorsqu'il s'agit de montrer ce genre d'égalité, de passer de \(cos\) à \(sin\), il faut pratiquer par changement de variable \(t=\pi/2-x\): \(\begin{align*} \begin{cases} t=\pi/2-x \\ dt = -dx\end{cases} \Rightarrow \begin{cases} t=0 \Rightarrow x=\pi/2 \\ t = \pi/2 \Rightarrow x= 0 \end{cases} \end{align*}\) \(\begin{align*} \forall n \in \mathbb N , I_n & = \int_{t=0}^{t=\pi/2} sin^nt.dt \\ \[\boxed{ \begin{align*} \forall n \in \mathbb N, I_n & =\int_0^{\pi/2}sin^nt .dt= \int_0^{\pi/2}cos^nt .dt \end{align*}}\] En calculant \(I_2\) de 2 façons , nous pouvons écrire que : \[\boxed{I_2 = \pi/4}\] |
4 - Montrer que \(I_n\) est convergente
|
Pour démontrer la convergence de \(I_n\), il faut:
calculer \(I_{n+1}-I_n\) :
Méthode plus analytique:
Minoration / majoration de \(I_n\)
Convergence de \(I_n\)
|
5 - Exprimer \(I_{n+2}\) en fonction de \(I_n\)
|
\(\begin{align*}\forall n \in \mathbb N, I_{n+2} &=\int_0^{\pi/2}sint^{n+2}t .dt \end{align*}\) On sent bien ici qu'il nous faut couper \(sint^{n+2}t\) en 2 morceaux pour faire une intégration par parties. Mais comment le découper:
Faisons une intégration par partie: \(\int u'v = [uv]- \int uv'\) Il ne faut pas oublier la "chain rule" quand on calcule \(v'\), c'est à dire le \(cos(t)\). \(\begin{align*}\forall n \in \mathbb N, \\ avec \(n+2 \neq 0\) car \(n \in \mathbb N\) Et pour finir, \[\boxed {\begin{align*}\forall n \in \mathbb N, I_{n+2} & = \frac{n+1}{n+2}I_n \end{align*}}\] |
6 - Exprimer \(I_{2p}\) et \(I_{2p+1 }\) en fonction de \(p\), \(\forall p \in \mathbb N\)
Calcul de \(I_{2p}\)
Calcul de \(I_{2p+1}\)
|
7 - Montrer que \(I_{n+1}\) est équivalent à \(I_n\) en \(+\infty\)
|
Pour montrer que \( I_{n+1}\) \( \widetilde{+ \infty}\) \( I_{n} \), montrons que \(\frac{I_{n+1}}{I_n} \space \widetilde{+\infty} \space1 \) Il faut commencer alors par montrer que \(\forall n \in \mathbb N, I_n \neq 0\) pour pouvoir diviser par \(I_n\) Sur \(]0;\pi/2]\),
Comme \(sin(t)\) n 'est pas la fonction constante égale à \(0\), alors son intégrale est strictement supérieure a \(0\) et \[\forall n \in \mathbb N, I_n \neq 0 \] \(I_n \) est décroissante (d'aprés la question 4) donc: \(\forall n \in \mathbb N\) \(\begin{align*} car \(\begin{align*} & \lim \limits_{n \to + \infty}\frac{n+1}{n+2}= \lim \limits_{n \to + \infty}\frac{1+\cancel{\frac{1}{n}}}{1+\cancel{\frac{2}{n}}} = 1\end{align*}\) D'après le Théorème des gengarmes: \(\lim \limits_{n \to + \infty}\frac{I_{n+1}}{I_{n}}=1\) et \(\frac{I_{n+1}}{I_{n}} \widetilde{+\infty }1\) et en définitive: \[ \boxed{\forall n \in \mathbb N, I_{n+1}\widetilde{+\infty }I_{n}}\] |
8 - Montrer que \(\forall n \in \mathbb N, (n+1)I_{n+1}I_{n} = \) Cte
|
La difficulté réside dans le fait que nous avons une suite constante, mais qui n 'a pas de nom. Donc nommons la en posant: \(\forall n \in \mathbb N, U_n= (n+1)I_{n+1}I_{n}\) et Calculons \(U_{n+1}\): \(\begin{align*}& \forall n \in \mathbb N, \\ Si \(\forall n \in \mathbb N, U_{n+1} = U_n\), alors \(U_n\) est constante. Quand on demande de démontrer que quelque chose est constant, il est toujours demandé implicitement de trouver cette constante. \[\boxed{ \forall n \in \mathbb N, (n+1)I_{n+1}I_{n}=\pi/2}\] |
9 - En déduire un équivalent simple de \(I_n\), puis sa limite
En conséquence: \((n+1)I_{n+1}I_{n} \space\widetilde{+ \infty} \space (n\times I_n \times I_n ) \\ \[\boxed{ I_n \space \widetilde{+ \infty} \space \sqrt{\frac{\pi}{2n}} }\] \(\lim \limits_{n \to + \infty}I_n = \lim \limits_{n \to + \infty} \sqrt{\frac{\pi}{2n}}=0\) \[\boxed {\lim \limits_{n \to + \infty}I_n=0} \] |