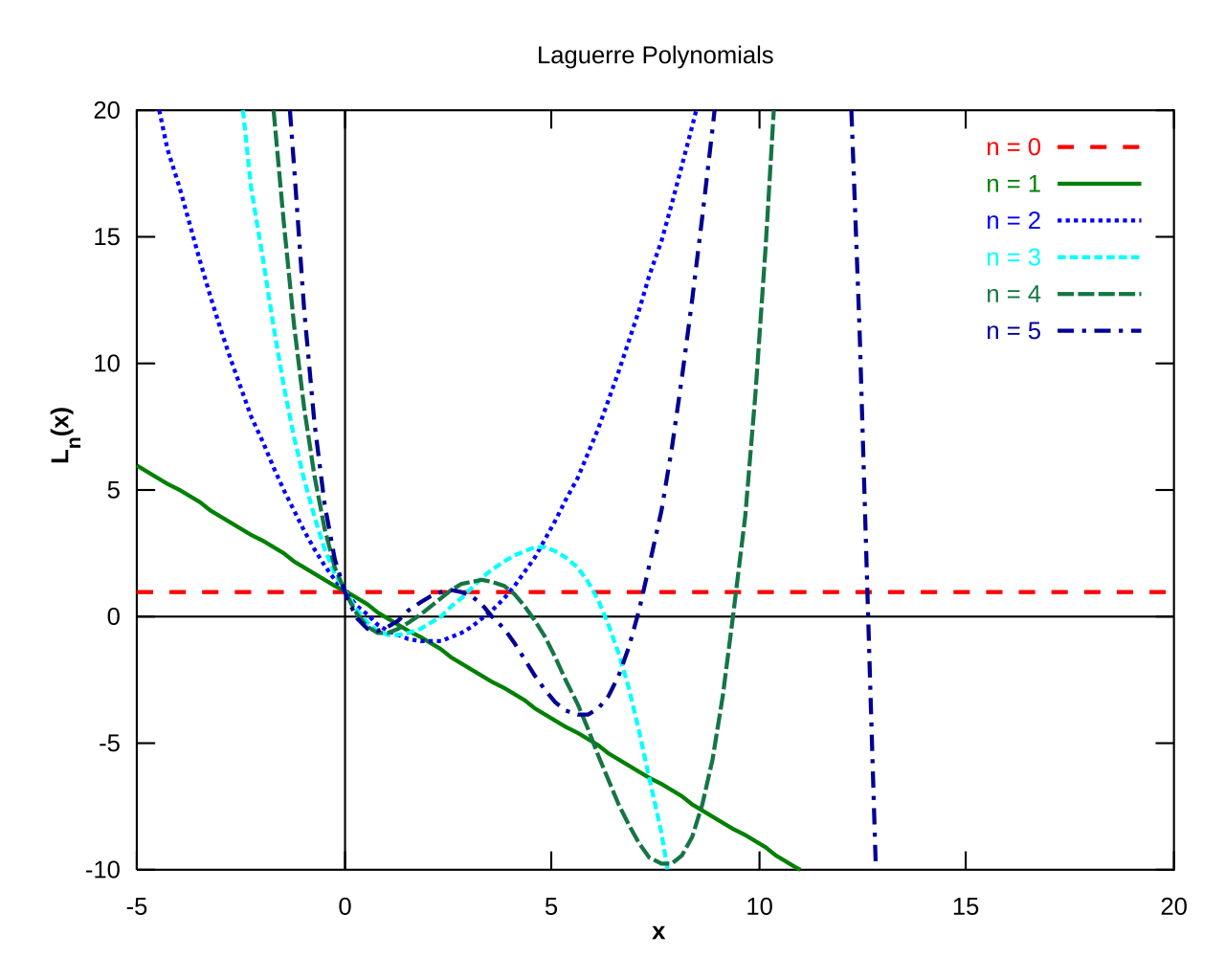
Les polynômes de Laguerre
8 - Soit \(J_n =n! \langle L_n,Q \rangle\). Montrer que \(\begin{align*}J_n = (-1)^k \int_0^{+\infty} ({e^{-x}x^n)}^{(n-k)} Q^{(k)}(x)dx \space \forall n \in \mathbb N^*, \space 0 \leq k \lt n \end{align*}\)
|
Rappels : \(\begin{align*} \begin{cases} \langle P,Q \rangle = \int_0^{+\infty}P(x)Q(x)e^{-x}dx \\ L_n(x) = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) } \\ \big[ (e^{-x} x^n)^{(k)} Q(x)\big]_0^{+\infty}=0 \space \underline{\forall n \in \mathbb N^*, \space 0 \leq k \lt n}, \space Q \in \mathbb R[X] \end{cases}\end{align*} \)
\(\begin{align*}J_n & = n! \langle L_n,Q \rangle =n! \int_0^{+\infty}L_n(x)Q(x)e^{-x}dx \\ \(\begin{align*}J_n & =\int_0^{+\infty} \underbrace{(x^n e^{-x} )^{ (n) }}_{u' }\underbrace{Q(x)}_{v}dx \\ Montrons cette relation par récurrence sur \(k\): \(0 \leq k \lt n \)
|
Sujet
|
Les polynômes de Laguerre sont des polynômes définis par : \(\begin{align*} L_n(x) = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) }\end{align*}\) ou (\(x^n e^{-x} )^{ (n) }\) est la dérivée nième de \(x^n e^{-x} \).
|
1 - Calculer \(L_0\), \(L_1\), \(L_2\)
|
\[\begin{align*} L_n(x) = \frac{e^x}{n!}(x^n e^{-x} )^{ (n) }\end{align*}\] \(\begin{align*} L_0(x) = \frac{e^x}{0!}(x^0 e^{-x} )^{ (0) } = e^x(1 \times e^{-x} )^{ (0) }=e^x \times e^{-x}=e^0 = 1\end{align*}\) \(\begin{align*} L_1(x) & = \frac{e^x}{1!}(x^1 e^{-x} )^{ (1) } = e^x(xe^{-x})' = e^x[e^{-x}-xe^{-x} ] \\ \(\begin{align*} L_2(x) & = \frac{e^x}{2!}(x^2 e^{-x} )^{ (2) } = \frac{e^x}{2}(x^2 e^{-x} )" = \frac{e^x}{2} \times [2x e^{-x}-x^2e^{-x}]' \\
|
2 - Montrer en utilisant la formule de Leiniz généralisée que \(\begin{align*} L_n(x) = \sum\limits_{k=0^n} \binom{n}{k}\frac{(-x)^k}{k!} \end{align*}\). Vérifier pour \(L_2\).
|
Formule de Leibniz généralisée :
Posons : \(f(x) = e^{-x} \) et \(g(x) =x^{n}\), alors \(f\) et \(g\) sont de classe \(C^\infty\). Calculons \(f^{(k)}\) et \(g^{(n-k)}\)
\(\begin{align*} L_2(x) & = \sum\limits_{k=0}^2 \binom{2}{k} \frac{-x^{k}}{k!} \\
|
3 - Remarquer que \(\forall n \in \mathbb N, \space L_n(0)=1\)
|
\(\begin{align*} L_n(x) = \sum\limits_{k=0}^n \binom{n}{k} \frac{(-x)^{k}}{k!} \end{align*}\) \(\begin{align*} L_n(0) & = \sum\limits_{k=0}^n \binom{n}{k} \frac{(0)^{k}}{k!} \\
En effet :\(L_0(0) = L_1(0) =L_2(0)=1\) |
4 - Montrer que \(\begin{align*} \forall n \in \mathbb N, \space I_n=\int_0^{+\infty} \frac{1}{n!}x^ne^{-x}dx =1 \end{align*}\)
|
\(\begin{align*} I_0 & =\int_0^{+\infty} \frac{1}{0!}x^0e^{-x}dx \\ Par récurrence: Soit la proposition \(P_n\): \(I_n=\int_0^{+\infty} \frac{1}{n!}x^ne^{-x}dx =1\)
|
5 - Montrer que pour \(\forall n \in \mathbb N; \space 0 \leq k \leq n, \space \big(e^{-x}x^n \big)^{(k)} = \big( \sum\limits_{j=n-k}^{n}a_jx^j \big)e^{-x}\)
|
On veut montrer que la dérivée de \(e^{-x}x^n\) , est de la forme \(e^{-x}Q(x)\), où \(Q(x)\) est un polynôme. Démontrons par récurrence sur \(k\):
|
6 - En déduire que \(\forall n \in \mathbb N^*, \space 0 \leq k \lt n\) et \(Q \in \mathbb R[X]\), on a : \(\big[ (e^{-x}x^n)^{(k)}Q(x)\big]_0^{+\infty}=0\)
|
Soit \(u(x) = (e^{-x}x^n)^{(k)}Q(x)\), \(\begin{align} \begin{cases} x e^{-x}P(x) \xrightarrow{x = 0} 0 \\ x e^{-x}P(x) \xrightarrow{x \to +\infty} 0 \text{ par croissance comparée} \end{cases} \Longrightarrow \big[ (e^{-x}x^n)^{(k)}Q(x)\big]_0^{+\infty}=0\end{align}\)
|
7 - Soit \(E= \mathbb R[X]\) muni de la fonction \(\begin{align*} (P,Q) \in E^2 \mapsto \langle P;Q \rangle = \int_0^{+\infty}P(x)Q(x)e^{-x}dx \end{align*}\). Montrer que \(\langle P,Q \rangle\) définit un produit scalaire.
1 - Existence de l'intégrale qui définit \(\langle P,Q \rangle\)
2 - Rappels de cours
3 - Forme symétrique :\(\langle P|Q \rangle = \langle Q|P \rangle\) ??
4 - Forme bilinéaire ??
5 - Forme définie positive ??
|
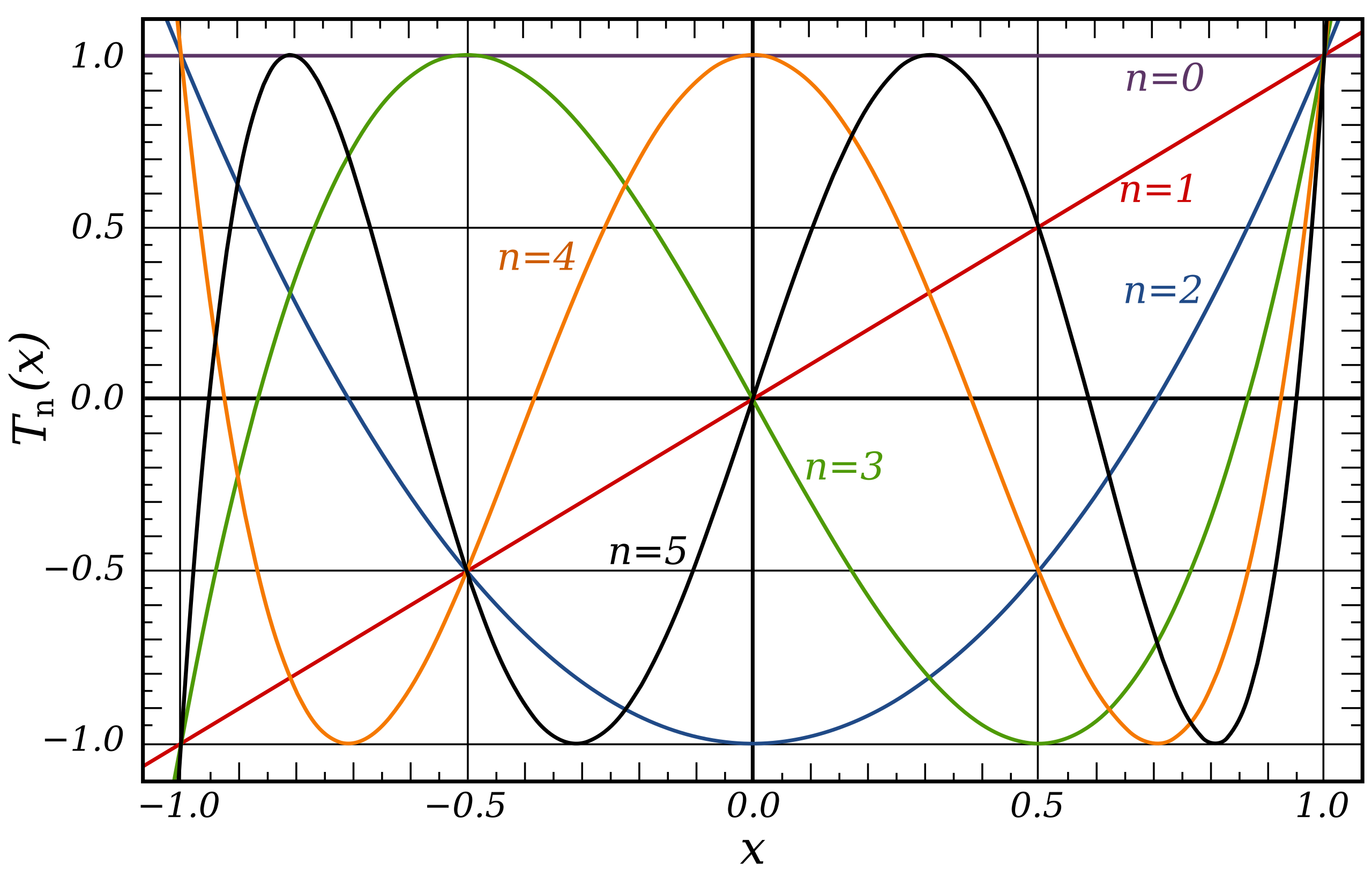
Les polynômes de Tchebychev
Sujet
|
|
1 - Donner les expression de \(T_0\), \(T_1\), \(T_2\), \(T_3\), \(U_1\),\(U_2\), \(U_3\)
|
On utilise les formules de trigonométrie usuelles:
|
2 - Montrer que les \(T_n\) et \(U_n\) existent, sont uniques, et sont donnés par:
\(\begin{align*} T_n(x) = \sum\limits_{k=0}^{\lfloor n/2 \rfloor} (-1)^k \binom{n}{2k} x^{n-2k}(1-x^2)^k \end{align*}\) et \(\begin{align*} U_n(x) = \sum\limits_{k=0}^{\lfloor (n-1)/2 \rfloor} (-1)^k \binom{n}{2k+1} x^{n-2k-1}(1-x^2)^k \end{align*}\)
1 - Existence:
2 - Unicité
3 - Conclusion :
|
||||||||||
3 - Montrer que \(\forall x \in [-1;1]\), \(T_n(x) = cos(n.arccos(x))\) et \(\forall x \in ]-1;1[\), \(U_n(x) = \frac{sin(n.arcos(x))}{\sqrt{1- x^2}}\)
|
On sait \( \begin{align*} \begin{cases} \cos(nt) = T_n(\cos t) \\ \sin (nt) = \sin{t} .U_n(\cos t) \end{cases} \end{align*}\) Soit: \( \begin{align*} \begin{cases}x \in [-1;1] \\
De même, soit: \(\begin{align*} \begin{cases} x \in ]-1;1[ \\
On remarque que:
Cette remarque sera utile dans des questions suivantes!! |
4 - Montrer que \(T'_n(x) = nU_n(x)\)
|
On sait : \( \begin{align*} \begin{cases} \cos(nt) = T_n(\cos t) \\ \sin (nt) = \sin{t} .U_n(\cos t) \end{cases} \end{align*}\) Dérivons \(cos(nt)\) de 2 façons différentes:
Par identification, il vient: Les fonctions polynômiales \(T'_n\) et \(n.U_n\) coïncident sur un ensemble infini, en l'occurrence l'ensemble des \(cos t\), \(t \in \mathbb R - k\pi \space (k \in \mathbb Z)\), donc ces 2 polynômes sont égaux. (voir la démonstration en question 2 pour l'unicité de \(T_n\) et \(U_n\) )
|
5 - Relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\)
|
Il existe plusieurs façons de poser le problème et d'y répondre:
1 - trouver une relation entre \(T_{n+1}\), \(T_{n}\), \(T_{n-1}\). C'est au candidat de trouver cette relation.
2 - Démontrer que \(\begin{align*} \forall X \in [-1;1], \space \space T_{n+1}(X)+ T_{n-1}(X) = 2X.T_n(X) \end{align*}\) par calcul direct
|
6 - En déduire les degré et coefficient dominant de \(T_n\)
|
Démonstrations par récurrence: 1 - le degré de \(T_n\) et de \(U_n\)
2 - Le coefficient dominant
3 - Confirmation avec la question 2
|
||||||
7 - Montrer que \(T_n\) a la même parité que \(n\)
|
On connait: \(\begin{align*} \begin{cases} T_0=1 \\ T_1=X \\ T_2=2x^2-1 \end{cases} \text{ et: } \begin{cases} \forall X \in [-1;1], \space & T_{n+1}(X) = 2X.T_n(X)- T_{n-1}(X) \\ \Leftrightarrow & T_{n+2}(X) = 2X.T_{n+1}(X)- T_n(X) \end{cases}\end{align*}\) Soit la proposition \(P_n\): "\(T_n \) a la même parité que \(n\)", qui peut aussi s'écrire \(\boxed{T_n(-X) = (-1)^nT_n(X)}\), ainsi:
|
8 - Montrer que \(\forall n \in \mathbb N\), \(T_n(1) = 1 \) , \(T'_n(1) = n^2\) , \(T_n(0)=0\) si \(n\) est pair, \(T_n(0) =(-1)^{n/2}\) sinon .
1 - \(\forall n \in \mathbb N\), \(T_n(1)=1\)
2 - \(\forall n \in \mathbb N\), \(T'_n(1)=n^2\)
3 - Montrer que \(T_n(0)=0\) si \(n\) est impaire et \(T_n(0)=(-1)^{n/2}\) sinon
|
9 - Montrer que pour \(n \in \mathbb N^*\), \(T_n\) possède \(n\) racines simples \(\begin{align*}x_k = cos \big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big)_{0 \leq k \leq n-1} \space , \space x_k \in [-1;1] \end{align*}\) et que \(\begin{align*} \sum\limits_{k=0}^{n-1}x_k=0 \end{align*}\)
|
Il s 'agit de trouver ici les racines du polynôme \(T_n(x)\) On pose: \( \begin{align*}T_n(cost) & = 0 \Leftrightarrow cos(nt) =0 \\
Il convient alors de retirer de l'ensemble des solutions tous les \(k \gt n\), ainsi on aura toujours \(0 \leq t \leq \pi \) Posons: \(t_k =\frac{\pi}{2n}+\frac{k \pi}{n}\) pour lesquels \(cos(nt_k)=0\). Alors la famille \(\big( t_k \big)_{k \in [\![ 0;n-1]\!] }\) contient exactement \(n\) éléments différents 2 à 2. \(T_n\) est un polynôme de degré \(n\) En conséquence , le polynôme \(T_n\) possède \(n\) racines simples \(x_k = cos(t_k)\) avec \(x_k \in [-1;1]\) et \(k \in [\![ 0;n-1]\!]\)
Si un polynôme \(P\) de degré \(n\) et de coefficient dominant \(a_n\) possède \(n\) racines simples \(x_i\) , alors on peut le mettre sous la forme \(P = a_n \prod\limits_{i=0}^{n}(X-x_i)\)
Donc \(a_{n-1}=0\) dans tout les cas et :
|
10 - Trouver les EXTREMA de \(T_n\)
|
Par définition: \(T_n(x) = T_n(cost) = cos(nt)\) Comme dans la question 9 : \(\begin{align*}\Leftrightarrow & \exists ? x \in \mathbb R \space \space / \space \space T_n(x) \text{ soit maximum} \\ On pose: \( \begin{align*}T_n(cost) \text{ est maximum }& \Leftrightarrow \lvert cos(nt) \rvert =1 \\
Posons: \(t'_k =k \pi\) pour lesquels \(\lvert cos(nt'_k) \rvert =1\). Alors la famille \(\big( t'_k \big)_{k \in [\![ 0;n]\!] }\) contient exactement \(n+1\) éléments différents 2 à 2. Nous avons donc trouvé les \(n+1\) extrema (différents 2 à 2) du polynôme \(T_n\)
|
11 - Montrer que \( \begin{align*} \prod\limits_{k=0}^{n-1}cos \bigg( \frac{\pi}{2n} + \frac{k\pi}{n} \bigg) \begin{cases} =0 \text{ si n est impair} \\ = \frac{(-1)^{n/2}}{2^{n-1}} \text{ si n est impair}\end{cases} \end{align*}\)
|
\(\begin{align*} \forall n \in \mathbb N^*, \space T_n(X) = 2^{n-1} \prod\limits_{k=0}^{n-1} \bigg[ X- cos\big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big) \bigg] \end{align*} \) \( \begin{align*}T_n(0) & = a_0 = 2^{n-1} \prod\limits_{k=0}^{n-1} \bigg[ 0- cos\big(\frac{\pi}{2n}+ \frac{k \pi}{n} \big) \bigg] \\ & = 2^{n-1} (-1)^n\prod\limits_{k=0}^{n-1} x_k \end{align*} \)
|
12 - Montrer que \(T_n\) est solution de l'équation différentielle: \((E): (X^2-1)y" + Xy' - n^2y=0\)
|
\(T_n\) est solution de (E) \(\Leftrightarrow (X^2-1)T"_n + XT'_n - n^2T_n=0\) On a: \(cos(nt) = T_n(cost)\) En dérivant une seconde fois, il vient: Nous avons un polynôme qui est nul pour une infinité de valeurs de \([-1;1]\). C 'est donc le polynôme identiquement nul. Et en conséquence, ce polynôme est nul quelque soit \(X \in \mathbb R\) et ( idem question 2 sur l 'unicité de \(T_n\)) :
|
13 - Soit \(E\) le \(\mathbb R\)-espace vectoriel des fonctions continues de \([-1;1]\) dans \(\mathbb R\). Justifier que l'application de \(E^2 \to \mathbb R\) définie par \(\langle f(t),g(t) \rangle = \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt\) est un produit scalaire.
1 - Existence de \(\begin{align*} \int_{-1}^{1}\frac{f(t)g(t)}{\sqrt{1-t^2}}dt = I \end{align*}\)
2 - \(\langle f,g \rangle\) est il un produit scalaire?
|
14 - Pour tous \((m,n) \in \mathbb N^2\), calculer le produit scalaire \(\langle T_n , T_m \rangle\). Que peut on dire de la famille \(\big(T_n\big)_{n \in \mathbb N}\) ?
|
\(\begin{align*} \langle T_n , T_m \rangle & = \int_{-1}^{1} \frac{T_n(x) T_m(x)}{\sqrt{1-x^2}} dx \end{align*}\) et \(T_n(cost) = cos(nt)\) Procédons à un changement de variable: \(\begin{align*} \langle T_n , T_m \rangle & = \int_{x=-1}^{x=1} \frac{T_n(x) T_m(x)}{\sqrt{1-x^2}} dx
Si \(m \neq m\), alors la famille \( \langle T_n , T_m \rangle = 0\) , alors \(\bigg(T_n \bigg)_{n \in \mathbb N}\) est une famille orthogonale de \(\mathbb R[X]\) au sens de \(\langle . , . \rangle\). La famille \( \langle T_n , T_m \rangle = 0\) , alors \(\bigg(T_n \bigg)_{n \in \mathbb N}\) n 'est pas normée.
|
15 - A partir du résultat de la question 4 et des autres résultats, déterminer les degré et coefficient dominant de \(U_n\)
|
Résultat de la question 4 : \(T'_n(X) = n.U_n(X)\) et donc \(U_n(X) =\frac{1}{n} T'_n(X)\)
|
16 - Montrer que \(\forall n \in \mathbb N, \exists t \in \mathbb R, \space U_n(cos t) = \frac{sin[(n+1)t]}{sint}\)
|
Dans la question 4 , on a démontré que \(T'_n=nU_n\) ou encore \(U_n = \frac{1}{n}T'_n\) On sait que \( T_n\) et \(cost\) sont de classe \(C^\infty\) et que \(T_n(cost) = cos(nt)\) En dérivant \(cos[(n+1)t]\): \( \big[ cos[(n+1)t] \big]' = -(n+1).sin[(n+1)t]\) En dérivant \(T_{n+1}(cost)\): \( \big[ T_{n+1}(cost) \big]' = -sint. T'_{n+1}(cost) \) Avec \( t \neq k \pi, \space k \in \mathbb Z\), il vient:
|
17 - En déduire que \(\big( U_n \big)_{n \in \mathbb N}\) suit aussi la relation de récurrence de la question 5, que \( \forall n \in \mathbb N, \space \space U_n\) est scindé simple sur \(\mathbb R\), à racine dans \(]-1;1[\), en précisant les racines
|
Soient \(n \in \mathbb N\) et \(t \in \mathbb R / \pi \mathbb Z\) On a: \(sin(a+b) +sin(a-b) = 2sina.cosb \Leftrightarrow sin(a+b) = 2sina.cosb - sin(a-b) \) On a d 'après la question 15: Tout comme l'unicité des polynômes \(\big( T_n)_{n \in \mathbb N}\) vue à la question 2 , les polynômes \(\big( U_n)_{n \in \mathbb N}\) sont eux aussi uniques.
si \(t \in \mathbb R\), \(U_n(cost) = 0 \Rightarrow sin[(n+1)t]= 0 \Rightarrow (n+1)t = k \pi \Rightarrow t = \frac{k \pi}{n+1}\) \(\forall k \in [\![ 1;n]\!] , \space \alpha_k = \frac{k \pi}{n+1}\) sont au nombre de \(n\) et sont distinctes. L'application \(cos\) est injective de \(]-1;1[\) vers \(]0;\pi[\), donc les \(cos(\alpha_k)\) sont distincts, et ce sont les racines de \(U_n\) Or , la relation : \(\forall n \in \mathbb N, \space U_{n+1} = \frac{1}{n+1}T'_{n+1}\)non montre que \(deg(U_{n+1}) = deg(T'_{n+1}) = n, donc possède n racines, ce qui montre que \)U_n$ est scindé simple. |
Les Polynômes de HERMITE
Les polynômes d'Hermite sont une suite de polynômes qui a été nommée ainsi en l'honneur de Charles Hermite. Ils sont parfois décrits comme des polynômes osculateurs. Ces polynômes apparaissent dans de nombreux champs d'application Ils sont parfois décrits comme des polynômes osculateurs. (un polynôme osculateur ou osculatoire est un polynôme fournissant une « bonne approximation » d'une fonction). Ils viennent généraliser les polynômes de Lagrange.
SUJET
|
Soit \((H_n)_{n \in \mathbb N}\), la famille de polynômes (dite de Hermite) défiie par :
|
1 - Démontrer que \(\begin{align*} \forall n \in \mathbb N\end{align*}\), \(H_n\) est un polynôme unitaire de degré \(n\)
|
\(\begin{align*} \begin{cases} H_0=1 \\ H_{n+1}= xH_n-H'_n \end{cases} \end{align*}\) et en effet \(\begin{align*} \begin{cases} H_0=1 \\ H_{1}= x \times 1-0 = x \\ H_2 = x \times x-1= x^2-1\\ \vdots \end{cases} \end{align*}\) Démonstration par récurrence:Soit la proposition \(P_n\): \(H_n\) est un polynôme unitaire de degré n
|
2 - Démontrer que \(\begin{align*} \forall n \in \mathbb N \end{align*}\), \(\begin{align*} H'_{n+1}=(n+1)H_n\end{align*}\)
|
\(\begin{align*} \begin{cases} H_0=1 \\ H_{n+1}= xH_n-H'_n \end{cases} \end{align*}\) Démonstration par récurrence:Soit la proposition \(P_n\) : \(\begin{align*} H'_{n+1}=(n+1)H_n\end{align*}\)
|
3 - Justifier de l'existence de l'intégrale qui définit \(\langle P|Q \rangle\)
|
On a : \(\begin{align*} \begin{cases} \langle P|Q \rangle = \int_{- \infty}^{+ \infty}P(x)Q(x)f(x)dx \\ f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \gt 0 \text{ et } \int_{- \infty}^{+ \infty}f(x)dx=1 \text{ et } f(x) \text{ est paire} \end{cases} \end{align*}\) La fonction \(P(x)Q(x)f(x)\) est continue sur \(\mathbb R\) comme produit de fonctions continues.
\(I_1\) ,\(I_2\) ,\(I_3\) , étant toutes les 3 convergentes, alors, \(\langle P|Q \rangle = \int_{- \infty}^{+ \infty}P(x)Q(x)f(x)dx\) est convergente:
|
4 - Démontrer que \(\langle .|. \rangle\) définit un produit scalaire sur \(\mathbb R[X]\)
|
Préliminaire: \(E\) désigne un \(\mathbb R\) espace vectoriel
Remarques: \(\mathbb R [X]\) est l'espace vectoriel de dimension infinie, des polynômes à 1 variable et à coefficient dans \(\mathbb R\). Les opérations dans cet espace sont connues. La forme \(\langle P|Q \rangle\) existe bien. Nous l avons démontré dans la question 3 .
|
5 - Dans la suite , \(\mathbb R[X]\) sera muni du produit scalaire \(\langle P|Q \rangle\) et de la norme euclidienne \(|| P ||\) associée.
Démontrer que \(\begin{align*} \forall n \in \mathbb N\end{align*}\), \(\langle P|H_n \rangle=\langle P^{(n)} |H_0 \rangle\)
|
On sait : \(\begin{align*} \begin{cases} \begin{cases} H_0=1 \\ H_{n+1}= xH_n-H'_n \end{cases} \\ \text{par croissance comparée } \lim\limits_{x \to +/- \infty} P(x)Q(x)f(x) = 0 \end{cases} \end{align*}\) Démonstration par récurrence:Soit la proposition \(P_n\) : \(\langle P|H_n \rangle =\langle P^{(n)} |H_0 \rangle \)
|
6 - En déduire que \(\begin{align*} \forall n \in \mathbb N\end{align*}\), la famille \((H_0,H_1, ......, H_n)\) est une base orthogonale de \(\mathbb R_n[X]\)
|
\(E\) désigne un espace vectoriel préhilbertien réel. Et on note : \(\langle .|.>\) le produit scalaire et \(||.||\) la norme associés.
On sait : \(\begin{align*} \forall n \in \mathbb N, \space \langle P|H_n \rangle =\langle P^{(n)} |H_0 \rangle \\
\(\mathbb R_n[X]\) est l'ensemble des polynômes a une variable, de degré \( \leq n\). Cet ensemble est un espace vectoriel de dimension \(n+1\) dont une base canonique est \((1,X,X^2, \cdots , X^n)\). Un polynôme de degré \(n\) est une combinaison linéaire des éléments de cette base canonique de \(n+1\) éléments. Pour démontrer que \((H_0,H_1, ......, H_n)\) est une base de \(\mathbb R_n[X]\), il suffit de montrer qu'elle est soit libre , soit génératrice. On démontrera qu'elle est libre en montrant simplement qu'elle est orthogonale. (proposition 1 et Définition 2)
Soient \((i,j) \in \mathbb N\) , avec \(i \neq j\) . Calculons \(\langle H_i|H_j \rangle \) Remarque préliminaire: Si \(deg(P)= n\) et \(m \gt n\) alors \(P^{(n)}= constante\) et \(P^{(m)}=0\). Ce qui nous amène a discerner 2 cas:
\(\forall i \in \mathbb N, \space \forall j \in \mathbb N, \space i \neq j, \space \langle H_i|H_j \rangle=0\)
|
7 - Calculer \(||H_n||\), \(\begin{align*} \forall n \in \mathbb N \end{align*}\)
|
\(E\) désigne un espace vectoriel préhilbertien réel.
On sait : \(\begin{align*} \begin{cases} \forall n \in \mathbb N, \space \langle P|H_n \rangle = \langle P^{(n)} |H_0 \rangle \\
Par définition: \(||H_n|| = \sqrt{\langle H_n|H_n \rangle } \) et \( ||H_n||^2 = \langle H_n|H_n \rangle \) \( \begin{align*} ||H_n||^2 & = \langle H_n|H_n \rangle = \langle H_n^{(n)}|H_0 \rangle \\ En conséquence:
|
8 - Soit \(P(x)= x^3+x^2+x+1\).
Préciser les polynômes \(H_1\), \(H_2\), \(H_3\), puis déterminer 4 réels \(a_i\) (\(0 \leq i \leq 3\)) tels que \(\begin{align*} P = \sum_{i=0}^{i=3}a_iH_i \end{align*}\).
En déduire la distance \(d\) du polynôme au sous espace \(\mathbb R_0[X]\) des polynômes constants, c'est à dire la borne inférieure de \(||P-Q||\) lorsque \(Q\) décrit \(\mathbb R_0[X]\)
|
On sait: \(\begin{align*} \begin{cases}H_{n+1}= xH_n-H'_n \\ H_0=1 \end{cases} \end{align*}\)
Soit \((\mathbb R_3[X];||.||)\) un espace pré-hilbertien, en particulier un espace euclidien, (\(||.|| = \sqrt{\langle .|. \rangle}\) normé et \(\mathbb R_0[X]\) un sous espace vectoriel non vide de \(\mathbb R_3[X]\), de dimension finie:
Alors \(d(P,\mathbb R_0[X]) = \inf_{Q \in \mathbb R_0[X]}(P,Q) = || P-\mathbb R_0[X] ||\) avec \(\begin{cases} \mathbb R_3[X] =\mathbb R_0[X] \bigoplus \mathbb R_0[X]^\perp \\ P=P_{\mathbb R_0[X]} + P_{\mathbb R_0[X]^\perp} \end{cases}\) Comme \(P \in \mathbb R_3[X]\) alors \(||P-\mathbb R_0[X]|| = || \mathbb R_0[X]^\perp ||\) \(\begin{align*}P(x) = \underbrace{a_0H_0(x)}_{\in \mathbb R_0[X] } + \underbrace{a_1H_1(x) + a_2H_2(x) + a_3H_3(x)}_{ \Rightarrow \in \mathbb R_0[X]^\perp} \\
|
9 - Soit \(\begin{align*} n \in \mathbb N\end{align*}\). On note \(p\) le nombre de racines réelles (distinctes) d'ordre impair du polynôme \(H_n\), et \(a_1,a_2,......,a_p\) ces racines, et \(S\) le polynôme défini par \(\begin{align*} \begin{cases} S=1 \text{ si p = 0} \\ S = \prod_{i=1}^p (x-a_i) \text{ sinon} \end{cases} \end{align*}\). Démontrer que si \(p \lt n\) alors \(\langle S|H_n \rangle=0\)
|
10 - Démontrer que pour tout \(x \in \mathbb R, \space S(x)H_n(x) \geq 0\)
|
Tous les polynômes de \(\mathbb C[X]\) sont décomposables en éléments simples de degré 1. \(H_n = \prod(x-a_i)^{\lambda_i} \prod\underbrace{(x^2+\alpha_ix+\beta_i)^{\mu_i}}_{\Delta \lt 0}\) produit de polynômes unitaires puisque \(H_n\) est un polynôme unitaire. \( \lambda_i\) et \(\mu_i\) existent pour les racines multiples. Calculons \(S(x)H_n(x)\):
|
11 - En déduire que \(H_n\) à \(n\) racines réelles distinctes.
|
Démonstration par l'absurde: Supposons \(H_n\) n'a pas \(n\) racines distinctes réelles. La fonction \(S(x) H_n(x)f(x)\) est continue et de classe \(C^{\infty}\) comme le produit de fonctions \(C^{\infty}\) \(\begin{align*} \langle S|H_n \rangle & = \int_{- \infty}^{+ \infty} \underbrace{S(x) H_n(x)}_{\geq 0} \underbrace{f(x)}_{\gt 0}dx = 0 \end{align*} \) \(\mathbb R[X]\) est un anneau intègre: si un produit est nul , alors forcément soit \(S=0\) , soit \(H_n = 0\), ce qui est absurde car par définition : \(s \neq 0 \) et \(H_n \neq 0\)
|
P(x) = ax²+bx+c, Delta positif
| \[\begin{align*} I= \int \frac{1}{x^2-5x+6}dx \end{align*} \text{ et } \Delta \gt 0\] | ||||||
|
|
| Généralisation: \[\begin{align*} & I = \int \frac{1}{ax²+bx+c}dx \end{align*}\] | ||||
|
|
10 Techniques d'intégration
\(\begin{align*} I =\int f(x)dx \end{align*}\)
\(\begin{align*} I = \overbrace{\int}^{\text{Symbole} \\ \text{intégration}} \underbrace{f(x)}_{\text{intégrande}} \overbrace{dx}^{\text{variable} \\ \text{d'intégration}} \end{align*}\)
Nous recherchons une fonction \(F(x)\) dont la dérivée est égale à l 'intégrande \(f(x)\). Cette fonction \(F(x)\) est une des primitives de \(f(x)\).
La dérivée de \(F(x) \) est égale à \(f(x)\). Mais on remarque que la fonction \(F(x) + C\), avec \(C=\)constante, \(C \in \mathbb R\) est aussi une primitive particulière de \(f(x)\). Pour cette raison, on précisera toujours l'existence de cette constante lors du calcul d'une primitive.
\(\begin{align*} I =\int f(x)dx = F(x)+C\end{align*}\), avec \(C \in \mathbb R \)
Nous allons voir dans les sous chapitres les règles d'intégration (calcul de primitive) essentielles.