|
\(\begin{align*} I= \int_{-1}^{5} \lvert x-3\rvert dx \end{align*}\)
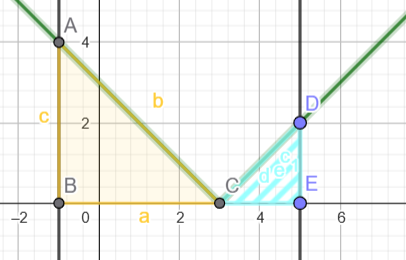 |
La fonction \(x \mapsto x-3\) est relativement simple. On peut la dessiner et en déduire le graphe de \(x \mapsto \lvert x-3 \rvert\). On s'aperçoiit alors que \(I\) est l'aire de 2 triangles limités par les droites d'équation \(\begin{cases} y=x-3 \\ y=-x-3 \\ x=-1 \\x=5 \end{cases} \).
Graphiquement , on détermine \(\begin{align*} I = \frac{4 \times 4}{2}+\frac{2 \times 2}{2}=10 \end{align*}\)
|
Pour rester dans le calculatoire , alors on peut passer par la relation de Chasles:
\(\begin{align*}
I & = \int_{-1}^{5} \lvert x-3\rvert dx \\
& = \int_{-1}^{3} \lvert x-3\rvert dx+\int_{3}^{5} \lvert x-3\rvert dx \\
& = \int_{-1}^{3} -x+3 dx+\int_{3}^{5} x-3 dx \\
& = [-\frac{x²}{2}+3x]_{-1}^{3} + [\frac{x²}{2}-3x]_{3}^{5} \\
& = (-\frac{9}{2}+9)-(-\frac{1}{2}-3) + (\frac{25}{2}-15)-(\frac{9}{2}-9) \\
& = -\frac{9}{2}+\frac{1}{2}+\frac{25}{2}-\frac{9}{2}+9+3-15+9 \\
& = \frac{8}{2}+6 \\
& = 4+6=10
\end{align*}\)
|

